Just a moment...
Just a moment...
/*Typography=========================== */ @import url('https://fonts.googleapis.com/css?family=Roboto:100,100i,300,300i,400,400i,500,500i,700,700i,900,900i'); html, body { width: 100%; height: auto; margin: 0; padding: 0; } .container { width: 90%!important; } a { text-decoration: none; color: #fff; } .dark { color: #222 !important; } .red { color: #ab2927; } .white { color: #fff !important; } .pagination a { padding: 0 10px; } .pagination strong { padding: 8px 20px; background: #39cbde; color: #fff; } .nav-links { margin: 0 20px; } .nav-links a { padding: 0 10px; } .nav-links span { padding: 8px 20px; background: #39cbde; color: #fff; } .cont { font-size: 15px; line-height: 21px; } .cont1 { font-size: 17px; line-height: 28px; } body { font-family: 'Roboto', sans-serif; position: relative; font-size: 14px; line-height: 24px; color: #000; } a { color: #6f6f6f; } a, a:active, a:focus, a:hover { outline: none; -webkit-transition: all 0.3s ease-in-out; -moz-transition: all 0.3s ease-in-out; -o-transition: all 0.3s ease-in-out; -ms-transition: all 0.3s ease-in-out; transition: all 0.3s ease-in-out; } a:hover { text-decoration: none; } h1, h2, h3, h4, h5, h6 { color: #3f3f3f; margin: 0 0 15px 0; font-weight: 500; } h1 { font-size: 48px; line-height: 52px; } h2 { font-size: 36px; line-height: 48px; } h3 { font-size: 30px; line-height: 36px; } h4 { font-size: 24px; line-height: 30px; } h5 { font-size: 18px; line-height: 24px; } h6 { font-size: 14px; line-height: 18px; } p { margin-bottom: 20px; } .section { padding: 50px 0; } nav.sticky.bootsnav ul.nav>li>a { color: #273272; } img.lazy { display: block; } /*Navbar Adjusment=========================== */ /* Navbar Atribute ------*/ .attr-nav>ul>li>a { /* padding: 28px 15px;*/ padding: 5px 8px 3px 10px; background: #E00; margin: 8px; border-radius: 5px; } .search i { font-size: 35px; color: #fff; } ul.cart-list>li.total>.btn { border-bottom: solid 1px #cfcfcf !important; color: #fff !important; padding: 10px 15px; } .solslider { padding-top: 170px; padding-bottom: 230px; } .sol-child-slider { padding-top: 170px; padding-bottom: 80px !important; } .tabs-left li { background: #f7f7f7; } active.tab-content::after { top: 16px; left: -50px; bottom: auto; border-width: 10px 50px 10px 0; border-color: transparent #f3961c; } .foothd { color: #fff; text-transform: uppercase; text-align: left; } .mx-1 { background: #fff !important; cursor: pointer; padding: 10px 14px !important; border-radius: 50%; } .mx-1:hover { background: #E00 !important; cursor: pointer; padding: 10px 14px !important; border-radius: 50%; } .container.text-center.text-md-left { padding-bottom: 48px; } .mx-1:hover i { color: #fff; } .footlnk li { text-align: left; } .footlnk li a { color: #fff; text-decoration: none; font-size: 15px; } .slider-texthome { font-size: 38px; color: #1B87CB; letter-spacing: 0; line-height: 50px; } .slider-textcont { font-size: 45px; color: #1B87CB; letter-spacing: 0; line-height: 60px; } p.text-rotator.leadtxt { font-size: 28px; padding: 0px 84px; line-height: 40px; margin-bottom: 20px; } .sliderlead { font-size: 20px; letter-spacing: 0; margin-top: 5px; margin-bottom: 7px; } .slider-text { font-size: 32px; font-weight: 700; line-height: 40px; } .txthead { font-size: 20px; line-height: 24px; font-weight: 700; } .w-100 { width: 46%!important; } .buttoncta {} .buttoncta a:hover { background: #ea1616; color: #fff; padding: 7px 13px; letter-spacing: 1px; text-transform: uppercase; font-weight: bold; text-decoration: none; border-radius: 5px; box-shadow: 2px 4px 7px 0px #484545; } .fancy { line-height: 0.5; text-align: left; margin-left: 115px; } .fancy span { display: inline-block; position: relative; } .fancy span:before { content: ""; position: absolute; height: 5px; border-bottom: 1px solid #DD0000; border-top: 1px solid #DD0000; top: 0; width: 100px; } .fancy span:before { right: 100%; margin-right: 15px; } .fancy span:after { left: 100%; margin-left: 15px; } nav.navbar .navbar-brand img.logo { width: 125px; background: #fff; } @media (min-width: 1024px) { /* Navbar General ------*/ nav.navbar ul.nav>li>a { padding: 30px 15px; font-size: 18px; font-weight: normal!important; } nav.navbar .navbar-brand { margin-top: 0; display: table; padding: 8px 0px; } nav.sticky .navbar-brand { margin-top: -14px; } nav.navbar .navbar-brand img.logo { background: #fff; } /* Navbar Center ------*/ nav.navbar-center .navbar-brand { margin: 0 !important; } /* Navbar Brand Top ------*/ nav.navbar-brand-top .navbar-brand { margin: 10px !important; } /* Navbar Full ------*/ nav.navbar-full .navbar-brand { position: relative; top: -15px; } /* Navbar Sidebar ------*/ nav.navbar-sidebar ul.nav, nav.navbar-sidebar .navbar-brand { margin-bottom: 50px; } nav.navbar-sidebar ul.nav>li>a { padding: 10px 15px; font-weight: bold; } /* Navbar Transparent & Fixed ------*/ nav.navbar.bootsnav.navbar-transparent.white { background-color: rgba(255, 255, 255, 0.3); border-bottom: solid 1px #bbb; } nav.navbar.navbar-inverse.bootsnav.navbar-transparent.dark, nav.navbar.bootsnav.navbar-transparent.dark { background-color: rgba(0, 0, 0, 0.3); border-bottom: solid 1px #555; } nav.navbar.bootsnav.navbar-transparent.white .attr-nav { border-left: solid 1px #bbb; } nav.navbar.navbar-inverse.bootsnav.navbar-transparent.dark .attr-nav, nav.navbar.bootsnav.navbar-transparent.dark .attr-nav { border-left: solid 1px #555; } nav.navbar.bootsnav.no-background.white .attr-nav>ul>li>a, nav.navbar.bootsnav.navbar-transparent.white .attr-nav>ul>li>a, nav.navbar.bootsnav.navbar-transparent.white ul.nav>li>a, nav.navbar.bootsnav.no-background.white ul.nav>li>a { color: #fff; } nav.navbar.bootsnav.navbar-transparent.dark .attr-nav>ul>li>a, nav.navbar.bootsnav.navbar-transparent.dark ul.nav>li>a { color: #eee; } } @media (max-width: 992px) { nav.navbar .navbar-brand img.logo { width: 100px; float: left; } /* Navbar General ------*/ nav.navbar .navbar-brand { margin-top: 0; position: relative; top: 4px; } .attr-nav>ul>li>a { padding: 10px; } /* Navbar Mobile slide ------*/ nav.navbar.navbar-mobile ul.nav>li>a { padding: 15px 15px; } nav.navbar.navbar-mobile ul.nav ul.dropdown-menu>li>a { padding-right: 15px !important; padding-top: 15px !important; padding-bottom: 15px !important; } nav.navbar.navbar-mobile ul.nav ul.dropdown-menu .col-menu .title { padding-right: 30px !important; padding-top: 13px !important; padding-bottom: 13px !important; } nav.navbar.navbar-mobile ul.nav ul.dropdown-menu .col-menu ul.menu-col li a { padding-top: 13px !important; padding-bottom: 13px !important; } /* Navbar Full ------*/ nav.navbar-full .navbar-brand { top: 0; padding-top: 10px; } } /* Navbar Inverse=================================*/ nav.navbar.navbar-inverse { background-color: #222; border-bottom: solid 1px #303030; } nav.navbar.navbar-inverse ul.cart-list>li.total>.btn { border-bottom: solid 1px #222 !important; } nav.navbar.navbar-inverse ul.cart-list>li.total .pull-right { color: #fff; } nav.navbar.navbar-inverse.megamenu ul.dropdown-menu.megamenu-content .content ul.menu-col li a, nav.navbar.navbar-inverse ul.nav>li>a { color: #eee; } nav.navbar.navbar-inverse ul.nav>li.dropdown>a { background-color: #222; } nav.navbar.navbar-inverse li.dropdown ul.dropdown-menu>li>a { color: #999; } nav.navbar.navbar-inverse ul.nav .dropdown-menu h1, nav.navbar.navbar-inverse ul.nav .dropdown-menu h2, nav.navbar.navbar-inverse ul.nav .dropdown-menu h3, nav.navbar.navbar-inverse ul.nav .dropdown-menu h4, nav.navbar.navbar-inverse ul.nav .dropdown-menu h5, nav.navbar.navbar-inverse ul.nav .dropdown-menu h6 { color: #fff; } nav.navbar.navbar-inverse .form-control { background-color: #333; border-color: #303030; color: #fff; } nav.navbar.navbar-inverse .attr-nav>ul>li>a { color: #eee; } nav.navbar.navbar-inverse .attr-nav>ul>li.dropdown ul.dropdown-menu { background-color: #222; border-left: solid 1px #303030; border-bottom: solid 1px #303030; border-right: solid 1px #303030; } nav.navbar.navbar-inverse ul.cart-list>li { border-bottom: solid 1px #303030; color: #eee; } nav.navbar.navbar-inverse ul.cart-list>li img { border: solid 1px #303030; } nav.navbar.navbar-inverse ul.cart-list>li.total { background-color: #333; } nav.navbar.navbar-inverse .share ul>li>a { background-color: #555; } nav.navbar.navbar-inverse .dropdown-tabs .tab-menu { border-right: solid 1px #303030; } nav.navbar.navbar-inverse .dropdown-tabs .tab-menu>ul>li>a { border-bottom: solid 1px #303030; } nav.navbar.navbar-inverse .dropdown-tabs .tab-content { border-left: solid 1px #303030; } nav.navbar.navbar-inverse .dropdown-tabs .tab-menu>ul>li>a:hover, nav.navbar.navbar-inverse .dropdown-tabs .tab-menu>ul>li>a:focus, nav.navbar.navbar-inverse .dropdown-tabs .tab-menu>ul>li.active>a { background-color: #333 !important; } nav.navbar-inverse.navbar-full ul.nav>li>a { border: none; } nav.navbar-inverse.navbar-full .navbar-collapse .wrap-full-menu { background-color: #222; } nav.navbar-inverse.navbar-full .navbar-toggle { background-color: #222 !important; color: #6f6f6f; } @media (min-width: 1024px) { nav.navbar.navbar-inverse ul.nav .dropdown-menu { background-color: #222 !important; border-left: solid 1px #303030 !important; border-bottom: solid 1px #303030 !important; border-right: solid 1px #303030 !important; } nav.navbar.navbar-inverse li.dropdown ul.dropdown-menu>li>a { border-bottom: solid 1px #303030; } nav.navbar.navbar-inverse ul.dropdown-menu.megamenu-content .col-menu { border-left: solid 1px #303030; border-right: solid 1px #303030; } nav.navbar.navbar-inverse.navbar-transparent.dark { background-color: rgba(0, 0, 0, 0.3); border-bottom: solid 1px #999; } nav.navbar.navbar-inverse.navbar-transparent.dark .attr-nav { border-left: solid 1px #999; } nav.navbar.navbar-inverse.no-background.white .attr-nav>ul>li>a, nav.navbar.navbar-inverse.navbar-transparent.dark .attr-nav>ul>li>a, nav.navbar.navbar-inverse.navbar-transparent.dark ul.nav>li>a, nav.navbar.navbar-inverse.no-background.white ul.nav>li>a { color: #fff; } nav.navbar.navbar-inverse.no-background.dark .attr-nav>ul>li>a, nav.navbar.navbar-inverse.no-background.dark .attr-nav>ul>li>a, nav.navbar.navbar-inverse.no-background.dark ul.nav>li>a, nav.navbar.navbar-inverse.no-background.dark ul.nav>li>a { color: #3f3f3f; } } @media (max-width: 992px) { nav.navbar.navbar-inverse .navbar-toggle { color: #eee; background-color: #222 !important; } nav.navbar.navbar-inverse .navbar-nav>li>a { border-top: solid 1px #303030; border-bottom: solid 1px #303030; } nav.navbar.navbar-inverse ul.nav li.dropdown ul.dropdown-menu>li>a { color: #999; border-bottom: solid 1px #303030; } nav.navbar.navbar-inverse .dropdown .megamenu-content .col-menu .title { border-bottom: solid 1px #303030; color: #eee; } nav.navbar.navbar-inverse .dropdown .megamenu-content .col-menu ul>li>a { border-bottom: solid 1px #303030; color: #999 !important; } nav.navbar.navbar-inverse .dropdown .megamenu-content .col-menu.on:last-child .title { border-bottom: solid 1px #303030; } nav.navbar.navbar-inverse .dropdown-tabs .tab-menu>ul { border-top: solid 1px #303030; } nav.navbar.navbar-inverse.navbar-mobile .navbar-collapse { background-color: #222; } } @media (max-width: 767px) { nav.navbar.navbar-inverse.navbar-mobile ul.nav { border-top: solid 1px #222; } div#indepe { top: 60px; } .section.section1.bannerhome { padding-top: 74px; } div#indepe .flag-txt p.offertxt.white.mb0 { line-height: 25px!important; font-size: .75em !important; letter-spacing: 0!important; } } /*Color=========================== */ nav.navbar.bootsnav ul.dropdown-menu.megamenu-content .content ul.menu-col li a:hover, .side .widget ul.link li a:hover, .side .widget ul.link li a:focus, .check-list li:before, ul.cart-list>li>h6>a, .attr-nav>ul>li>a:hover, .attr-nav>ul>li>a:focus, nav.navbar-sidebar ul.nav li.dropdown.on>a, nav.navbar-sidebar .dropdown .megamenu-content .col-menu.on .title, nav.navbar-sidebar ul.nav li.dropdown ul.dropdown-menu li a:hover, nav.navbar ul.nav li.dropdown.on>a, nav.navbar.navbar-inverse ul.nav li.dropdown.on>a, nav.navbar-sidebar ul.nav li.dropdown.on ul.dropdown-menu li.dropdown.on>a, nav.navbar .dropdown .megamenu-content .col-menu.on .title, nav.navbar ul.nav>li>a:hover, nav.navbar ul.nav>li.active>a:hover, nav.navbar ul.nav li.active>a, nav.navbar li.dropdown ul.dropdown-menu>li a:hover { color: #3dbcff; } nav.navbar.navbar-transparent ul.nav>li>a:hover, nav.navbar.no-background ul.nav>li>a:hover, nav.navbar ul.nav li.scroll.active>a, nav.navbar.navbar-dark ul.nav li.dropdown ul.dropdown-menu>li>a:hover, nav.navbar ul.nav li.dropdown.on>a, nav.navbar-dark ul.nav li.dropdown.on>a { color: #060606 !important; } @media(max-width:920px) { nav.navbar .dropdown .megamenu-content .col-menu ul>li>a:hover, nav.navbar.navbar-dark .dropdown .megamenu-content .col-menu .title:hover { color: #0082C6 !important; } } /*Border=========================== */ ul.cart-list>li.total>.btn { border-color: #0082C6; } nav.navbar li.dropdown ul.dropdown-menu { border-top-color: #fff !important; } /*Background=========================== */ ul.cart-list>li.total>.btn, .attr-nav>ul>li>a span.badge, nav.navbar .share ul>li>a:hover, nav.navbar .share ul>li>a:focus { background-color: #0082C6; } ul.cart-list>li.total>.btn:hover, ul.cart-list>li.total>.btn:focus { background-color: #dc3236 !important; } /*Accordion Menu*/ #accordion1 .panel, #accordion5 .panel, #accordion3 .panel, #accordion4 .panel { border-bottom: 2px solid #c3c3c3!important; border-color: transparent; background: transparent!important; } #accordion1 .collapsed, #accordion5 .collapsed, #accordion3 .collapsed, #accordion4 .collapsed { background: transparent!important; } #accordion1 .panel-default>.panel-heading, #accordion5 .panel-default>.panel-heading, #accordion3 .panel-default>.panel-heading, #accordion4 .panel-default>.panel-heading { background: transparent!important; } .panel-group .panel { border-radius: 8px; box-shadow: none; border-color: none; } .panel-default>.panel-heading { padding: 0; border-radius: 8px; color: #212121; background-color: #FAFAFA; border-color: #EEEEEE; } .panel-title { font-size: 14px; } .panel-title>a { display: block; padding: 3px 15px; text-decoration: none; border-radius: 28px; font-size: 17px; letter-spacing: 0px; } .more-less { float: right; color: #212121; } .panel-default>.panel-heading+.panel-collapse>.panel-body { border-top-color: #EEEEEE; } .more-less { top: 8px !important; font-weight: bold !important; } .navbar-toggle.collapsed { background: transparent !important; /* color: #fff !important;*/ } .collapsed { background: #f7f7f7; color: #444 !important; } .collapsed>.more-less { color: #fff !important; font-weight: bold !important; } .nav.nav-justified>li>a { position: relative; } .nav.nav-justified>li>a:hover, .nav.nav-justified>li>a:focus { background-color: transparent; } .nav.nav-justified>li>a>.quote { position: absolute; left: 0px; top: 0; opacity: 0; width: 30px; height: 30px; padding: 5px; background-color: transparent; border-radius: 15px; color: #fff; } .nav.nav-justified>li.active>a>.quote { opacity: 1; } /*.nav.nav-justified > li > a > img { box-shadow: 0 0 0 5px #EE0000; }*/ .nav.nav-justified>li>a>img { max-width: 100%; opacity: .3; -webkit-transform: scale(.8, .8); transform: scale(.8, .8); -webkit-transition: all 0.3s 0s cubic-bezier(0.175, 0.885, 0.32, 1.275); transition: all 0.3s 0s cubic-bezier(0.175, 0.885, 0.32, 1.275); } .nav.nav-justified>li.active>a>img, .nav.nav-justified>li:hover>a>img, .nav.nav-justified>li:focus>a>img { opacity: 1; -webkit-transform: none; transform: none; -webkit-transition: all 0.3s 0s cubic-bezier(0.175, 0.885, 0.32, 1.275); transition: all 0.3s 0s cubic-bezier(0.175, 0.885, 0.32, 1.275); } .tab-pane .tab-inner { padding: 30px 0 20px; } @media (min-width: 768px) { .nav.nav-justified>li>a>.quote { left: auto; top: auto; right: 45%; bottom: 25px; font-size: 50px; } #nav-tabs .active .lead2 { color: #E00 } } .section5 .nav.nav-justified>li>a>.quote { left: auto; top: auto; right: 45%; bottom: 68px; font-size: 50px; } .solli { display: inline; float: left; } .solli li { text-align: left; font-size: 16px; } .fancy2 { line-height: 0.5; text-align: left; margin-left: 115px; } .fancy2 span { display: inline-block; position: relative; } .fancy2 span:before { content: ""; position: absolute; height: 5px; border-bottom: 1px solid #fff; border-top: 1px solid #fff; top: 0; width: 100px; } .fancy2 span:before { right: 100%; margin-right: 15px; } .fancy2 span:after { left: 100%; margin-left: 15px; } .fancy3 { line-height: 0.5; text-align: left; margin-left: 61px; } .fancy3 span { display: inline-block; position: relative; } .fancy3 span:before { content: ""; position: absolute; height: 5px; border-bottom: 1px solid #1B87CB; border-top: 1px solid #1B87CB; top: 0; width: 50px; } .fancy3 span:before { right: 100%; margin-right: 15px; } .fancy3 span:after { left: 100%; margin-left: 15px; } /*Fade content bs-carousel with hero headersCode snippet by maridlcrmn (Follow me on Twitter @maridlcrmn) for Bootsnipp.comImage credits: unsplash.com*/ /********************************/ /* Fade Bs-carousel */ /********************************/ .fade-carousel { position: relative; height: 100vh; } .fade-carousel .carousel-inner .item { height: 100vh; } .fade-carousel .carousel-indicators>li { margin: 0 2px; background-color: #DB0000; border-color: #DB0000; opacity: .7; } .fade-carousel .carousel-indicators>li.active { width: 10px; height: 10px; opacity: 1; } /********************************/ /* Hero Headers */ /********************************/ .hero2 { padding-top: 10%; } .hero3 { padding-bottom: 20%; } .hero { position: absolute; vertical-align: middle; bottom: 0%; left: 7%; z-index: 3; color: #fff; text-align: left; /*text-transform: uppercase; -webkit-transform: translate3d(-50%,-50%,0); -moz-transform: translate3d(-50%,-50%,0); -ms-transform: translate3d(-50%,-50%,0); -o-transform: translate3d(-50%,-50%,0); transform: translate3d(-50%,-50%,0);*/ } .hero h1 { font-size: 4em; font-weight: bold; margin: 0 0 10px 0; padding: 0; color: #fff; text-align: left; } .hero h3 { font-size: 2em; color: #fff; text-align: left; font-weight: bold; margin: 5px 0 0 0; padding: 0; } .fade-carousel .carousel-inner .item .hero { opacity: 0; -webkit-transition: 2s all ease-in-out .1s; -moz-transition: 2s all ease-in-out .1s; -ms-transition: 2s all ease-in-out .1s; -o-transition: 2s all ease-in-out .1s; transition: 2s all ease-in-out .1s; } .fade-carousel .carousel-inner .item.active .hero { opacity: 1; -webkit-transition: 2s all ease-in-out .1s; -moz-transition: 2s all ease-in-out .1s; -ms-transition: 2s all ease-in-out .1s; -o-transition: 2s all ease-in-out .1s; transition: 2s all ease-in-out .1s; } /***slider2*****************************/ .full-screen { background-size: cover; background-position: center; background-repeat: no-repeat; } /* Overlay */ /********************************/ /********************************/ /* Custom Buttons */ /********************************/ .btn.btn-lg { padding: 10px 40px; } .btn.btn-hero, .btn.btn-hero:hover, .btn.btn-hero:focus { color: #f5f5f5; background-color: #1abc9c; border-color: #1abc9c; outline: none; margin: 20px auto; } /********************************/ /* Slides backgrounds */ /********************************/ .fade-carousel .slides .slide-1, .fade-carousel .slides .slide-2, .fade-carousel .slides .slide-3, .fade-carousel .slides .slide-4, .fade-carousel .slides .slide-5 { height: 100vh; background-size: cover; background-position: center center; background-repeat: no-repeat; } /*.fade-carousel .slides .slide-1 { background-image: url(https://ununsplash.imgix.net/photo-1416339134316-0e91dc9ded92?q=75&fm=jpg&s=883a422e10fc4149893984019f63c818); }.fade-carousel .slides .slide-2 { background-image: url(https://ununsplash.imgix.net/photo-1416339684178-3a239570f315?q=75&fm=jpg&s=c39d9a3bf66d6566b9608a9f1f3765af);}.fade-carousel .slides .slide-3 { background-image: url(https://ununsplash.imgix.net/photo-1416339276121-ba1dfa199912?q=75&fm=jpg&s=9bf9f2ef5be5cb5eee5255e7765cb327);}*/ #bs-carousel .carousel-indicators { margin-bottom: 36px; } nav.navbar.bootsnav ul.nav>li>a { padding: 18px 15px; font-size: 16px; } ul.phone-strip { display: block; width: auto; float: left; margin: 0px; padding: 17px 0px; background: #eee; color: #000; font-size: 16px; } ul.phone-strip li { list-style: none; float: left; padding: 0 20px; color: #000; } li.mob-btn { background: #ab2927; border-radius: 18px; line-height: 28px; color: #fff; width: 138px; text-align: center; margin: 14px 0px 14px 14px; } ul.mega-menulist li { padding: 4px 12px; font-size: 13px; } ul.mega-menulist li:hover { background: #f0f0f0; color: #962321; } ul.nav.nav-pills.nav-stacked li:hover a:before { font-weight: bold; color: #ab2927; } ul.nav.nav-pills.nav-stacked li a:before { /*font-family: 'FontAwesome';*/ content: '►'; float: right; font-size: 16px; color: #cbcbcb; margin-left: 10px; } ul.nav.nav-pills.nav-stacked li a { font-size: 13px!important; padding: 0px 0px!important; text-align: left!important; } .tab-pane .tab.col-md-6 { border: 0px; width: 50%; float: left; background: #efefef; min-height: 341px; } span.tablinks a:hover li:after { font-weight: bold; color: #ab2927; } span.tablinks a li:after { /*font-family: 'FontAwesome';*/ content: '►'; float: right; font-size: 16px; color: #cbcbcb; margin-left: 10px; } ul.dropdown-menu.mega-menu { min-width: 700px!important; left: 0px; transform: translate(-50%); background: #fff!important; background-size: contain!important; border-bottom: 4px solid #ab2927!important; } ul.mega-menulist { border-right: 1px solid #e8e8e8; padding: 0px 0px; list-style: none; margin: 0px; } ul.mega-menulist2 { border-right: 0px; } .mega-menu .padding0 { padding-left: 0px; padding-right: 0px; } /********************************/ /* Media Queries */ /********************************/ @media screen and (min-width: 980px) { .hero { width: 980px; } } @media screen and (max-width: 640px) { .hero h1 { font-size: 4em; } } /* Responsive Media Queries max 480px*/ @media screen and (max-width: 480px) { nav.navbar { padding-top: 7px !important; } nav.sticky .navbar-brand img.logo { background: none !important; padding: 10px; min-height: 45px; } } /* Change background color of buttons on hover */ .tab button:hover { background-color: #ddd; } /* Create an active/current "tab button" class */ .tab button.active { background-color: #00b1e5; color: #fff; } /* Style the tab content */ .tabcontent { float: left; padding: 30px 0px; width: 64%; border: none; } .tab { float: left; width: 33%; margin-left: 0%; } .tab button.active:after { left: 100%; top: 50%; border: solid transparent; content: " "; height: 0; width: 0; position: absolute; pointer-events: none; border-color: rgba(238, 238, 238, 0); border-right-color: #eee; border-width: 10px; margin-top: -10px; transform: rotate(-180deg); border-color: rgba(19, 175, 235, 0); border-right-color: #00b1e5; } a.notxtdec { text-decoration: none; } .mb10 { margin-bottom: 10px; } .mt0 { margin-top: 0px !important; } .mb0 { margin-bottom: 0px !important; } /*****JT CSS*****/ nav.navbar.bootsnav ul.nav>li>a { color: #000; } .navbar-default .navbar-nav>li>a:focus, .navbar-default .navbar-nav>li>a:hover { color: #ab2927!important; background-color: transparent; } .navbar { position: relative; min-height: 58px!important } nav.navbar.bootsnav ul.nav>li.dropdown>a.dropdown-toggle:after { color: #ab2927; } div#navbar-menu { margin-top: 0px; } li.signline { position: relative; } li.signline:after { position: absolute; top: 50%; right: 0px; content: ''; width: 2px; height: 20px; background: #ab2927; transform: translate(0, -50%); } .bannerhome p.slider-text.white { position: relative; } /*.bannerhome p.slider-text.white:after { content: ''; background: #ffffff57; height: 2px; width: 100px; position: absolute; left: 0px; bottom: -120px;}*/ .headbutton { padding: 8px 18px; border: 3px solid #ffffff; border-radius: 58px; color: #fff; text-align: center; background: #000; font-size: 13px; font-weight: 700; } .headbutton1 { padding: 8px 18px; border: 3px solid #ffffff; border-radius: 58px; color: #fff; text-align: center; background: #ab2927; font-size: 13px; font-weight: 700; width: 160px; } .kln { width: 100%; float: left; margin-top: 80px; } .blog-img-width, .feat img { width: 100%; height: 147px; } .getcall-box { border: 0px; border-radius: 0px; text-align: center; padding: 10px; width: 100%; float: right; /*margin-top: -5%;*/ } .getcall-box h3.slider-text2 { font-size: 20px; font-weight: bold; position: relative; padding-left: 22px; text-align: left; letter-spacing: 0; } .getcall-box h3.slider-text2:after { content: ''; background: #eeb617; left: 0px; position: absolute; width: 4px; height: 30px; top: 50%; transform: translate(0, -50%); } .getcall-box button.buttonctadarkbtn.btn.btn-lg { box-shadow: 5px 4px 3px #bbb0b0; width: 100%; margin-top: 20px; } .tab-img button.buttonctadarkbtn.btn.btn-lg { padding: 6px 40px; } .instr-bx { background: #f7f7f7; width: 100%; float: left; border-radius: 48px; padding: 18px 0px; font-size: 18px; font-weight: 700; line-height: 28px; text-align: center; position: absolute; bottom: -92px; box-shadow: 1px 10px 10px 1px #d6d6d6; } .inst2 { width: 100%; border: 1px solid #fff; padding: 16px 0px; color: #fff; } .section18 { padding: 30px 0px; } .rgt-icon p.cont2.mb0 { line-height: 48px; font-size: 17px; } .getcall-box p.cont2.dark { font-size: 14px; text-align: left; } .getcall-box input.form-control { border: 0px; border-bottom: 2px solid #868686; border-radius: 0px; box-shadow: none; } .getcall-box input.form-control:focus { border-bottom: 2px solid #ab2927; box-shadow: none; } /*button.buttonctadarkbtn.btn { border-radius: 58px; background: #ab2927; color: #fff; font-size: 17px; font-weight: 700;}*/ button.buttonctadarkbtn.btn { border-radius: 58px; box-shadow: none !important; background: #ab2927; color: #fff; font-size: 17px; font-weight: 700; } .btn.btn-lg { padding: 6px 40px; } .tablink1 { background-color: transparent; color: black; float: left; border: none; outline: none; cursor: pointer; padding: 0 0 8px 0px; font-size: 18px!important; width: 18%; border-bottom: 4px solid #444; margin: 0 12px; font-weight: 700; } .tablink1:hover { border-bottom: 4px solid #ab2927; } .tablink1:active { border-bottom: 4px solid #ab2927; } /****tab classes *****/ .register ul.nav.nav-tabs { width: 400px; margin: 0 auto; border: 0px; text-align: center; } .register ul.nav.nav-tabs li.nav-item { display: table; margin: 0 auto; width: 200px; text-align: center; } .register ul.nav.nav-tabs li.nav-item a.nav-link { padding: 10px 30px; font-size: 17px; color: #ffffff; background: #b12c27; /* border-radius: 4px; */ border: 0px; box-shadow: 1px 1px 8px 1px #eee; /*padding: 10px 30px; font-size: 17px; color: #040404; background: #fff; border-radius: 4px; border: 0px; box-shadow: 1px 1px 8px 1px #c5bdbd75;*/ } .register ul.nav.nav-tabs li.nav-item.active a { /*box-shadow: inset 1px 2px 12px #00000052; background: #ab2927; color: #fff;*/ box-shadow: inset 1px 2px 12px #eee; background: #ffffff; color: #a92927; } .register .nav-tabs>li.active>a, .register .nav-tabs>li.active>a:focus, .register .nav-tabs>li.active>a:hover { color: #fff; cursor: default; background-color: #02b5e1; border: 0px!important; } .responsive { line-height: 20px; background: #fff; padding: 10px; } .td-start { width: 100%; float: left; border-bottom: 1px solid rgba(151, 151, 151, 0.1); padding: 10px 0px; display: flex; align-items: center; font-weight: 700; box-shadow: 1px 1px 8px 1px #eee; } .td-txt { width: 100%; float: left; border-bottom: 1px solid rgba(151, 151, 151, 0.1); padding: 10px 0px; display: flex; align-items: center; } .td-txt4 { background: #f7f7f7; } .btn-store1 { padding: 2px 16px !important; text-transform: none !important; letter-spacing: 0px !important; font-size: 12px !important; font-weight: 800; } .btn-store2 { background: #B12C27 none repeat scroll 0 0 !important; border-radius: 18px !important; color: #fff !important; cursor: pointer; display: inline-block; font-family: inherit; font-size: 13px !important; font-weight: 300; margin: 0 10px 10px 0; outline: medium none; padding: 2px 14px; position: relative; text-decoration: none; } .btn-store { background: #EEB617 none repeat scroll 0 0 !important; border-radius: 18px !important; color: #fff !important; cursor: pointer; display: inline-block; font-family: inherit; font-size: 13px !important; font-weight: 300; letter-spacing: 1px; margin: 0 10px 10px 0; outline: medium none; padding: 12px 10px 12px; position: relative; text-decoration: none; text-transform: uppercase; transition: all 0.3s ease-out 0s; } td { text-align: center; vertical-align: middle; width: 238px; color: #77808a; padding: 13px 0; } .durtd strong { font-size: 16px; color: #000; font-weight: 900 !important; } .timetd strong { font-size: 16px; color: #000; font-weight: 900 !important; } .hd th { vertical-align: text-top; text-align: center; font-size: 16px; padding: 10px; } .hd th { vertical-align: text-top; text-align: center; border-bottom: 1px solid #e4e4e4 !important; } .hd { padding: 7px 0; border: none; } .schdl { font-family: "montserrat"; } .headingseaction { font-size: 22px !important; font-weight: bold; margin-bottom: 10px; color: #ffffff; border-left: 5px solid #eda900; padding-left: 24px; } .enrolltd { border-right: none; } th { border: none !important; } .button-area { margin: -21px auto 0px auto; text-align: center; } .button-area1 { background: white; padding: 8px 48px; font-size: 18px; font-weight: 600; border: none; border-radius: 4px; margin: 0 auto; width: auto; box-shadow: 1px 1px 8px 1px #eee; } .tab { overflow: hidden; border: 1px solid #ccc; background-color: #f1f1f1; } .tabcontent { display: none; width: 100%; } .singl-hov { background: #fff; width: 100%; float: left; padding: 10px 10px; } .singl-hov ul.Real li { padding: 0px 2px; color: #444; text-align: left; } nav#heder .singl-hov p.mb0 { padding: 8px 10px; text-align: left; font-size: 17px; } .singl-hov p.mb0 { padding: 8px 10px; text-align: left; } .singl-hov ul.Real { width: 100%; float: left; border-top: 1px solid #eee; padding: 10px 2px 10px 25px; } ul.Real li { color: #000; font-size: 12px; line-height: 17px; } .singl-hov p.btn-cour { border: 1px solid #eee; width: 140px; float: left; font-size: 14px; font-weight: 700; padding: 8px; line-height: 14px; margin-top: 14px; background: #FFC107; } nav#heder .singl-hov span.btn-cour { float: none; padding: 5px 10px; border: 1px solid #eee; width: 140px; font-size: 14px; font-weight: 700; line-height: 14px; background: #FFC107; margin: 0px; } .btn-bx { width: 100%; float: left; margin-top: 14px; } .singl-hov ul.Real li:hover { background: #fff; } .tab-pane .tabcontent { float: left; border-left: none; display: none; width: 100%; padding: 0px; } nav#heder .whtpprpost { box-shadow: 4px 4px 1px 0px #ddd; background: #fff; border: solid 1px #ddd; padding: 5px; border-radius: 5px; -webkit-transition: ease .02s; transition: ease .02s; } .btn-cour { list-style: none; float: left; padding: 0px 20px; display: table; width: 100%; text-align: center; border: 1px solid #fff; margin-bottom: 20px; } .singl-hov ul.Real a.btn-cour { color: #000; } span.icon-nav { display: block; box-shadow: 0px 2px 7px 2px #eee; border-radius: 50%; width: 70px; height: 70px; margin: 0 auto 10px auto; padding: 12px 0px; } span.icon-nav img { margin: 0 auto; } #Course p.slider-cont.blue { margin-bottom: 48px; font-size: 16px; } .course:after { content: ''; background: #eeb617; left: 0px; position: absolute; width: 4px; height: 30px; top: 50%; transform: translate(0, -50%); } .button-area1:focus { outline: -webkit-focus-ring-color auto 0px!important; } /* bhoechie tab */ div.bhoechie-tab-container { z-index: 10; background-color: #ffffff; padding: 0 !important; border-radius: 4px; -moz-border-radius: 4px; border: 1px solid #ddd; margin-top: 20px; margin-left: 0px; -webkit-box-shadow: 0 6px 12px rgba(0, 0, 0, .175); box-shadow: 0 6px 12px rgba(0, 0, 0, .175); -moz-box-shadow: 0 6px 12px rgba(0, 0, 0, .175); background-clip: padding-box; opacity: 0.97; filter: alpha(opacity=97); } div.bhoechie-tab-menu { padding-right: 0; padding-left: 0; padding-bottom: 0; } div.bhoechie-tab-menu div.list-group { margin-bottom: 0; } div.bhoechie-tab-menu div.list-group>a { margin-bottom: 23px; border: 0px; box-shadow: 1px 1px 8px 1px #eee; border-right: 3px solid #444444; } div.bhoechie-tab-menu div.list-group>a .glyphicon, div.bhoechie-tab-menu div.list-group>a .fa { color: #5A55A3; } div.bhoechie-tab-menu div.list-group>a:first-child { border-top-right-radius: 0; -moz-border-top-right-radius: 0; } div.bhoechie-tab-menu div.list-group>a:last-child { border-bottom-right-radius: 0; -moz-border-bottom-right-radius: 0; } div.bhoechie-tab-menu div.list-group>a.active, div.bhoechie-tab-menu div.list-group>a.active .glyphicon, div.bhoechie-tab-menu div.list-group>a.active .fa { background-color: #f7f7f7; border: 0px; color: #333; margin-bottom: 23px; border-right: 3px solid #ab2927; } div.bhoechie-tab-menu div.list-group>a.active:after { content: none; position: absolute; left: 100%; top: 50%; margin-top: -6px; border-left: 0; border-bottom: 8px solid transparent; border-top: 8px solid transparent; border-left: 8px solid #f7f7f7; } div.bhoechie-tab-content { box-shadow: 1px 1px 8px 1px #eee; padding: 16px 20px; height: 428px; overflow: scroll; } div.bhoechie-tab-content::-webkit-scrollbar { width: 4px; height: 8px; } div.bhoechie-tab-content::-webkit-scrollbar-thumb { border-radius: 0px; background-color: rgb(171, 41, 39); } div.bhoechie-tab div.bhoechie-tab-content:not(.active) { display: none; } .form-head { font-size: 12px; color: white; letter-spacing: 0; margin-top: -24px; width: 114px; background: #444; line-height: 25px; float: left; text-align: left; padding-left: 10px; } div.bhoechie-tab-menu div.list-group>a.active p.form-head { background: #eda900; font-weight: bold; color: #fff; } div.bhoechie-tab-menu p.cont2 { font-weight: bold; margin-top: 12px; } div.bhoechie-tab-content ul { margin: 0px; padding: 0px 0px; list-style: none; } div.bhoechie-tab-content ul li { padding: 4px 0px; color: #3c3c3c; } .tab-img { background: #f7f7f7; box-shadow: 1px 1px 8px 1px #eee; padding: 20px 0; } .tab-img img { width: 92%; margin: 14px auto 14px auto; } div.bhoechie-tab-menu div.list-group:after { background: #ab2927; position: absolute; top: 0px; content: ''; width: 3px; height: 400px; left: 68px; z-index: -1; } span.icon-nav img { margin: 0 auto; width: 50px; } .tablink1 a { color: black; } .crm { background: #3598c1; color: #fff; padding: 24px 10px; height: 192px; } .crm p.slider-text.white, .million .counter p.slider-text.white { /* font-size: 48px; */ font-size: 35px; } .million { background: #414a53; color: #fff; padding: 24px 10px; height: 192px; } .half { background: #fff; padding: 38px 0px; box-shadow: 1px 1px 8px 1px #eee; } .half img { width: 330px; margin: 0 auto 10px auto; } .wehave { margin: 54px 0 0 -50px; background: #f7f7f7; box-shadow: 1px 1px 8px 1px #eee; padding: 54px 70px; } .percentage { background: #f7f7f7; color: #414a53; padding: 10px 10px; box-shadow: 1px 1px 8px 1px #eee; } .still { background: #fff; width: 92%; margin: 0 auto; } i.fa.fa-sort-down.pull-right { font-size: 30px; line-height: 20px; color: #3598c1; } .percentage .counter p.slider-text { font-size: 80px; margin-top: 20px; color: #414a53; } .doyou { background: #f7f7f7; color: #360d0e; padding: 20px 10px; box-shadow: 1px 1px 8px 1px #eee; width: 100%; float: left; } .doyou p { font-size: 16px; line-height: 28px; } .jobsare { width: 100%; float: left; background: #414a53; position: relative; padding-top: 14px; } .asper { width: 100%; float: left; position: relative; } .jobsare p.slider-text.white { position: absolute; top: 50%; transform: translate(-50%, -50%); right: -20px; } .doyou button.buttonctadarkbtn.btn.btn-md a.dark.notxtdec { color: #fff!important; font-size: 14px; padding: 8px 11px; } .asper p.cont.white.mb0 { margin: 11px 0px; line-height: 22px; } .grace { width: 100%; float: left; background: #f7f7f7; } .grace img { border-radius: 50%; box-shadow: 1px 1px 8px 1px #eee; width: 100px; height: 100px; } .grace-bx { width: 100%; float: left; overflow: scroll; height: 310px; margin-top: 20px; background: #f7f7f7; padding: 20px 0px; } .still p.slider-text.dark { font-size: 35px; line-height: 35px; color: #585353!important; } p.nophone { font-size: 28px; font-weight: 700; color: #585353; text-align: center; margin-top: 20px; } .wehave p.slider-text.dark { font-size: 25px; font-weight: 700; line-height: 32px; } .grace-bx::-webkit-scrollbar-thumb { border-radius: 0px; background-color: rgb(171, 41, 39); } .grace-bx::-webkit-scrollbar { width: 4px; height: 8px; } .still { background: #fff; width: 92%; margin: 0 auto 20px auto; border-radius: 8px; padding: 21px 10px; } .still.maria p.slider-text.dark { font-size: 28px; font-weight: normal; } .still.maria span.red { font-size: 24px; font-weight: bold; } .btn.active.focus, .btn.active:focus, .btn.focus, .btn:active.focus, .btn:active:focus, .btn:focus { outline: none!important; } input:-internal-autofill-selected { font-size: 16px; font-weight: 700; } select.custom-select.form-control { border: 0px; border-bottom: 2px solid #868686; border-radius: 0px; box-shadow: none; margin-bottom: 10px; width: 24%; float: left; margin-right: 16px; padding: 0px; } select.custom-select2.form-control { border: 0px; border-bottom: 2px solid #868686; border-radius: 0px; box-shadow: none; margin-bottom: 0px; width: 100% !important; float: left; margin-right: 16px; padding: 0px; } p.lead4.red { font-size: 24px; font-weight: 700; line-height: 28px; padding: 4px 0; } .lead1 { font-size: 20px; font-weight: 700; position: relative; padding-left: 14px; text-align: left; } .viewall-bx { width: 100%; float: left; padding: 10px 20px; } .viewall { color: #13617D; border-radius: 5px; font-size: 14px; } span.viewall a { color: #13617D; text-decoration: underline; } .lead1:after { content: ''; background: #eeb617; left: 0px; position: absolute; width: 4px; height: 30px; top: 50%; transform: translate(0, -50%); } .lead2 { font-size: 22px; font-weight: 700; } .lead3 { font-size: 20px; font-weight: 700; position: relative; padding-left: 14px; text-align: left; } .lead3:after { content: ''; background: #eeb617; left: 0px; position: absolute; width: 4px; height: 30px; top: 50%; transform: translate(0, -50%); } .slider-cont { font-size: 17px; line-height: 21px; } .cont2 { font-size: 15px; line-height: 20px; } .cont3 { font-size: 14px; line-height: 24px; } .still p.slider-text.dark { font-size: 27px; line-height: 29px; color: #585353!important; } .star-rating-review i.fa.fa-star { color: #FFC107; } ul.social { list-style: none; } li.fb-icon { background: url(https://www.janbasktraining.com/assets/demo2019/img/sprite-JT.webp); width: 40px; height: 40px; float: left; margin-right: 8px; background-position: 0px 2px; } li.tw-icon { background-position: -55px 2px; } li.ld-icon.fb-icon { background-position: -116px 2px; } li.yu-icon.fb-icon { background-position: -173px 2px; } .footer-copyright.text-center.py-3.mb0.white { background: #000; padding: 10px; } ul.list-unstyled.footlnk li { padding: 4px 0px; } ul.list-unstyled.footlnk { padding: 14px 0px; } .lineon { position: relative; line-height: 46px; } .lineon:after { position: absolute; bottom: 0px; background: #fff; width: 40px; height: 2px; left: 0px; content: ''; } .lineon:before { position: absolute; top: 48px; background: #777; width: 1px; height: 110px; right: 14px; content: ''; } .lineon1 { position: relative; line-height: 46px; } .lineon1:after { position: absolute; bottom: 0px; background: #fff; width: 40px; height: 2px; left: 0px; content: ''; } .whtlogo img { margin-top: 20px; } .star-rating-review { margin: 0 auto; width: 100%; text-align: center; } .tab-bx:after, .register:after { position: absolute; content: ''; background: transparent; width: 280px; height: 280px; right: -180px; border-radius: 50%; border: 30px solid #e4e4e4db; top: -60px; } .tab-bx, .register { position: relative; } #Course { position: relative; } div#Course:after { position: fixed; content: ''; background: transparent; width: 280px; height: 280px; left: -110px; border-radius: 50%; border: 30px solid #e4e4e4db; bottom: 30px; z-index: -1; } .star-rating-review i.fa.fa-star.greystar { color: #848484!important; } .so-iconbx { position: relative; border-radius: 50%; } .so-icon { position: absolute; left: 0px; top: 40px; border-radius: 8px; box-shadow: 0px 1px 8px 1px #44444475; } .so-icon .test { position: absolute; width: 30px; top: 0px; transform: translate(-50%); left: 50%; background: #fff; border-radius: 50%; padding: 2px; height: 30px; box-shadow: 1px 1px 8px 1px #6d6d6d; } .test a { font-size: 12px; } span.fa-stack:nth-of-type(1) { position: relative; top: 50%; left: 50%; transform: translate(-50%, -50%); } span.fa-stack.fa-lg { color: #4f598f; } .grace p.lead2.dark { font-size: 18px; margin-bottom: 6px; } .grace p.lead2.red.mb0 { line-height: 38px; } .careericon { width: 50px; height: 50px; float: left; border: 1px dashed #ffffff; border-radius: 50%; text-align: center; line-height: 44px; position: absolute; left: 30px; top: -30px; background: #b12c27; } .careericon img { width: 26px; } .counter { padding: 20px 0; border-radius: 5px; } .count-text { font-size: 13px; font-weight: normal; margin-top: 10px; margin-bottom: 0; text-align: center; } .fa-2x { margin: 0 auto; float: none; display: table; color: #4ad1e5; } .instr-bx i { display: none; } :focus { outline: -webkit-focus-ring-color auto 0px; } .faq-acor #accordion1 .panel.panel-default { border-radius: 0px; } .faq-acor #accordion1 .panel-heading { border-radius: 0px; } .mobilescreen { display: none; } .modal { z-index: 1111111!important; } .inst2 i.fa { float: left; margin-right: 8px; line-height: 24px; display: block; font-size: 14px; color: #ffffff; } .rgt-icon { width: 64%; margin: 0 auto; } .dat { font-size: 14px; font-weight: 700; margin-bottom: 0px; } .est { font-size: 10px; margin-bottom: 0px; } #Course .course.red { font-size: 27px; font-weight: 700; position: relative; padding-left: 14px; text-align: left; line-height: 28px; } .iconav { width: 42px; height: 42px; /*background: url(https://www.janbasktraining.com/assets4/demo2019/img/sprite-JT.webp);*/ background-position: -391px -7px; margin-right: 7px; } span.iconav.iconav1 { background-position: -343px -7px; } span.iconav.icona2 { background-position: -298px -7px; } span.iconav.icona3 { background-position: -252px -7px; } span.iconav.iconav4 { background-position: -441px -7px; } span.iconav.iconav5 { background-position: -485px -7px; } .cert { font-size: 28px; font-weight: 700; position: relative; padding-left: 28px; } .select2-container { box-sizing: border-box; display: inline-block; margin: 0; position: relative; vertical-align: middle; z-index: 999999; border: 0px; border-bottom: 2px solid #868686; border-radius: 0px; box-shadow: none; margin-bottom: 0px; width: 24%!important; float: left; margin-right: 16px!important; padding: 0px; background: transparent; } span.select2-selection.select2-selection--single { background-color: white!important; border: 0px!important; border-radius: 5px 0 0 5px; height: 32px!important; } } label.error { color: red; font-weight: normal; font-size: 12px; line-height: 10px; } div#thankyou1 { z-index: 111111; } div#thankyou1 .modal-content { background-image: -webkit-gradient(linear, left top, right bottom, from(#02b3e4), to(#02ccba)); background-image: linear-gradient(to bottom right, #fff4f8, #8ac4f3); margin: auto; padding: 20px 0px; border: 1px solid #888; width: 80%; } #accordion1 .panel-title>a, #accordion3 .panel-title>a, #accordion4 .panel-title>a, #accordion5 .panel-title>a, #accordion6 .panel-title>a { font-weight: normal; } #layout62 .counter { padding: 8px 0; } #layout62 .percentage p.slider-text { font-size: 70px; line-height: 20px; } #layout62 .wehave { margin: 26px 0 0 -50px; } #layout62 .instr-bx { bottom: -142px; } #layout63 .jobsare p.slider-text.white { font-size: 28px; font-weight: 700; line-height: 40px; } #layout63 .asper p.cont.white.mb0 { margin: 11px 0px; line-height: 22px; font-size: 14px; } #layout63 h4.lead3.white.hlf { font-size: 18px; } #layout63 .instr-bx { width: 828px; } .sticky-nav-tab h2 { color: #000; font-size: 17px; font-weight: normal; line-height: 20px; display: flex; -webkit-box-pack: center; -ms-flex-pack: center; justify-content: center; -webkit-box-align: center; -ms-flex-align: center; align-items: center; -webkit-box-flex: 1; -ms-flex: 1; padding: 0px; margin: 0px; letter-spacing: 0px; } /*Blog CSS*/ .mb0 { margin-bottom: 0px !important; } .mt50 { margin-top: 50px !important; } .crsbox { background: #f7f7f794; display: inline-block; padding: 20px 10px 2px 10px; box-shadow: -1px 2px 10px 0px rgba(0, 0, 0, 0.15); } .crsbox p { margin-bottom: 12px; } .crsbox img { width: 40px; } .blogttl { font-size: 15px; padding: 10px; box-shadow: 0 5px 20px 2px rgba(0, 0, 0, .12); font-weight: bold; margin-bottom: 10px; } .catrdmr { font-size: 16px; vertical-align: bottom; text-decoration: underline; } .crsbox2 { box-shadow: 0 5px 20px 2px rgba(0, 0, 0, .12); overflow: hidden; width: 100%; float: left; position: relative; } .crsbox2 p { position: absolute; bottom: -20px; left: 50%; color: #fff; font-size: 18px; text-align: center; width: 100%; transform: translate(-50%); background: rgba(0, 0,0,0.7); } ul.breadcrumb.dark { margin-top: -20px; margin-bottom: 24px; background: #f7f7f7; padding: 8px 10px; } ul.breadcrumb.dark li a { color: #444; } ul.breadcrumb.dark li a:active { color: #ab2927; } .rghtsideblg p { margin-bottom: 12px !important; line-height: 19px; } .rghtsideblg p a { color: #000 !important; } .rght { background: #f7f7f7; display: block; padding: 20px 14px; box-shadow: 3px 3px 0px #00000024; } .breadcrumb { padding: 0px; margin-bottom: 10px; list-style: none; background-color: transparent; border-radius: 4px; color: #fff; } .breadcrumb li a { color: #f7f7f7; } .video-responsive { overflow: hidden; padding-bottom: 56.25%; position: relative; height: 0; } .video-responsive iframe { left: 0; top: 0; height: 100%; width: 100%; position: absolute; } .techblog { font-size: 18px; } .blogbannercta { font-size: 15px; } .blogdtlright h2 { font-size: 2em; line-height: 48px; letter-spacing: 0px; color: #333; text-align: left; } .blogdtlright h3 { font-size: 2em; line-height: 48px; letter-spacing: 0px; color: #333; text-align: left; } .blogdtlright li { font-size: 1em; line-height: 1.5em; text-align: left; padding-bottom: 10px; } .blogdtlright table { width: 100% !important; margin: 10px auto; display: inline-table; } .blogdtlright td { text-align: left; vertical-align: middle; width: 238px; color: #000; padding: 5px 14px; border: solid 1px #ddd; font-size: 15px; } .hglhter { padding: 1em; background: #f7f7f7; box-shadow: 1px 2px 4px 0px #00000038; margin: 0; width: 100%; display: block; font-weight: bold; border: 0!important; border-left: 4px solid #34495E!important; text-align: left; margin-bottom: 10px; } pre { text-align: left; } .crtfdbutton { background: #333 !important; padding: 5px 15px !important; border-radius: 18px; line-height: 28px; color: #fff !important; text-align: center; margin: 14px 0px 14px 14px; } .crtfdbutton:hover { background: #333 !important; padding: 5px 15px !important; border-radius: 18px; line-height: 20px !important; color: #fff !important; text-align: center; margin: 14px 0px 14px 14px; } .progress-container { width: 100%; height: 5px; background: #f7f7f7; } .progress-bar { height: 5px; background: #A32122; width: 0%; } /*we will use the :before element to show numbers*/ /****Blogs****/ .blogdtlright { font-size: 1em; line-height: 1.7em; text-align: justify; margin-bottom: 10px; } .blogdtlright img { margin: 0px auto 10px auto; /*margin: 10px auto 10px auto;*/ display: table; } .getcall-box.panel-default img.img-responsive { margin: 0px auto; } .blogdtlright h1 { font-size: 32px; font-weight: 700; line-height: 40px; } .blogdtlright h2 { font-size: 26px; font-weight: 600; color: #337ab7; line-height: 30px; margin-top: 20px; margin-bottom: 10px; } .blogdtlright h3 { font-size: 21px; font-weight: 600; line-height: 30px; color: #000; margin-top: 20px; margin-bottom: 10px; } .blogdtlright h4 { font-size: 18px; font-weight: 500; line-height: 25px; margin-top: 20px; color: #000; letter-spacing: 0; margin-bottom: 10px; } .blogdtlright h5 { font-size: 16px; font-weight: 700; line-height: 28px; margin-top: 20px; color: #337ab7; margin-bottom: 10px; } .blogdtlright h6 { font-size: 14px; font-weight: 700; line-height: 28px; color: #337ab7; margin-top: 20px; margin-bottom: 10px; } .blogdtlright a { color: #337ab7; } .sti{ margin-top:0px !important; margin-bottom:0px !important;} .blogttl p { text-align: initial; min-height: 67px; line-height: 20px; margin-bottom: 0px !important; } .blogdtlright img:nth-child(1) { /*width: 100%;*/ } .blogttl p a { border-bottom: none; color: #23527c; } .blogttl p a:hover { border-bottom: none; color: #444; } a u.rd { border-bottom: none!important; } table tr:nth-child(odd) { background: #d4d0d04d; } table tr:nth-child(even) { background: #f7f7f7; } .cmt_pro { border-radius: 50%; box-shadow: 5px 2px 5px #00000052; width: 120px; overflow: hidden; } .section.section1.bannerhome { background-size: cover; } img.img-responsive.post_thumb { width: 100%; } form#comment_form textarea.form-control:focus { border-bottom: 2px solid #ab2927; -webkit-box-shadow: inset 0 1px 1px rgba(0, 0, 0, .075), 0 0 8px rgba(177, 177, 177, 0.6); box-shadow: inset 0 1px 1px rgba(0, 0, 0, .075), 0 0 8px rgba(220, 220, 220, 0.6); /* -webkit-box-shadow: none; */ border-top: 0px; border-left: 0px; border-radius: 0px; } form#comment_form button.buttonctadarkbtn.btn.btn-lg { width: 280px; } .comment_dtl ul { width: 100%; } .getcall-box.panel-default a { border-bottom: none; font-weight: 400; } .featured_img img { width: 100%; margin-bottom: 20px; } .sed { /* width: 84px; height: 84px; border-radius: 50%; background: #512DA8; font-size: 35px; color: #fff; text-align: center; line-height: 84px;*/ width: 48px; height: 48px; line-height: 50px; font-size: 22px; float: left; border-radius: 50%; background: #512DA8; color: #fff; text-align: center; } .sedtxt h3 { margin-top: 0px !important; } .sedtxt p { margin-bottom: 5px !important; } /*.rplybtn { border: solid 1px #000 !important; padding: 0 10px; font-weight: 500; }*/ .getcall-box.panel-default li.fb-icon { width: 32px !important; height: 23px !important; } .rplybtn { background: #ab2927; border: 0px!important; color: #fff !important; font-size: 12px; padding: 4px 14px; text-align: center; border-radius: 28px; line-height: 15px; margin-top: 5px; float: none !important; } .time-change-wrapper { background: #B62626; color: #fff; padding: 6px; display: inline-table; margin-bottom: 0px !important; } .blogdtlright ul, ol { margin-top: 10px; } .blogdtlright pre { margin: 10px 0 10px 0px; font-size: 16px; } .singlcours { box-shadow: 0 5px 20px 2px rgba(0, 0, 0, .12); font-weight: bold; border-bottom: solid 2px #999; } .getcall-box .singlcours h3.coursetitle { text-align: center; padding: 5px 0; margin: 0px; } .getcall-box .singlcours p.links.headbutton2.white { border: none !important; line-height: 19px; font-size: 13px !important; font-weight: 500; background: #ab2927 !important; margin: 8px 6px 8px 0px; border-radius: 5px; } .getcall-box .singlcours .row.courseelmnt { margin-left: 0!important; margin-right: 0; } .browsecate ul { list-style: none; margin: 0px; padding: 0px; } .browsecate ul li { float: left; box-shadow: 0 0px 8px 0px rgb(232, 232, 232); font-weight: bold; border-bottom: solid 1px #4a7dc5; margin-right: 10px; font-size: 15px; text-align: center; padding: 4px 10px; margin-top: 6px; margin-bottom: 6px; } .section.section4.trend { padding-bottom: 10px; } /*3719 Css START*/ #rgthfiltrbtn button.buttonctadarkbtn.btn, #rgthfiltrbtn a.buttonctadarkbtn.btn { border-radius: 58px; box-shadow: none !important; background: #ab2927; color: #fff; font-size: 13px; font-weight: 700;padding: 3px 24px; } #rgthfiltrbtn a.buttonctadarkbtn.btn {background: #333; } #topfiltrbtn button.buttonctadarkbtn.btn, #topfiltrbtn a.buttonctadarkbtn.btn { border-radius: 58px; box-shadow: none !important; background: #ab2927; color: #fff; font-size: .95em; font-weight: 700; padding: 9px 16%; } #topfiltrbtn a.buttonctadarkbtn.btn {background: #333; border: solid 1px #fff;} .rghtsideblg p {} .thumbdt, .thumbview, .thumbrdmr, .crsprc, .crstm { font-size:0.8em} .lead5{ font-size:1.05em;} .mb5{ margin-bottom:5px !important;} .mtb8{ margin:8px 0 !important;} #msg2{color: #3c763d; text-align: left; background: #fbfbfb; border: solid 1px #ddd; border:none; font-size: .9em; padding: 0 5px; margin-top: 8px; font-weight: bold;} #email-error, #name-error, #mobile-error{ color: #ab2927; text-align: left; background: #fbfbfb; font-size: .8em; padding: 0 5px; margin-top: 8px; font-weight: 500; } @media screen and (max-width: 480px) { .blog-img-width, .feat img { width: 100%; height: auto !important; }} /*3719 Css END*/ /*23-9-2019 Blogs Css */ .pre1 { width: 94%; background: #fff!important; border: 0px!important; display: table; margin: 0 auto; position: relative; } .pre1 h4 { position: absolute; left: 43%; top: -18px; transform: translate(-50%,0); box-shadow: 1px 0px 8px 2px #e8e8e8; margin-bottom: 20px; padding: 4px 10px; background: #337ab7; color: #fff; font-size: 16px; border-radius: 4px; } .pre1 ul li a { border: 0px; font-size: 15px; font-weight: 700; } .pre1 ul li a:before { color: #001e30; content: "\21FE"; display: inline-block; font-family: 'ionicons'; margin-left: -24px; width: 24px; font-weight: bold; } .pre1 ul li ul li a:before { content:none; } .pre1 ul li:before { background: rgba(189,189,189,.4); bottom: 13px; display: block; left: 50px; position: absolute; top: 13px; width: 2px; } .pre1 ul { width: 100%; float: right; background: #fbfbfbc9; padding: 40px 10px 30px 48px; list-style-position: inside; box-shadow: 3px 3px 0px 0px #00000024; margin-right: 20px; list-style: none; border-top: 3px solid #00000024; border-left: 3px solid #00000024; } .pre1 ul li ul { width: 100%; box-shadow: none; margin: 0px; padding: 0px; border-top: 0px; border-left:0px; } .pre1 ul li ul li{ font-size: 13px; padding: 0px 20px; border-left: 0px; border-bottom: 0px; margin-bottom: 0px; position: relative; border-left: solid 2px #ab2927; color:#444; } .pre1 ul li ul li a{ font-size: 13px; color: #444; } .pre1 ul li ul li:before { position: absolute; left: 0px; top: 44%; content: ''; background: #ab2927; width: 16px; height: 1px; transform: translate(0,-50%); } .pre1 ul li ul:after{ content:none; } .pre1 ul li { padding-bottom: 4px; position: relative; border-bottom:1px solid #c3c3c3; padding-left: 10px; margin-bottom: 5px; float: left; width: 100%; } /*.pre1 ul:after { position: absolute; left: -66px; top: 30px; content: ''; background: url(https://www.janbasktraining.com/blogs/assets/img/blogbxs.jpg) top center no-repeat; background-size: cover; width: 24%; height: 92%; background-position: -22px 0px; }*/ .pre1:after { position: absolute; left: 50%; bottom: 2px; content: ''; background: #337ab7; width: 95%; height: 10px; transform: translate(-50%,0%); border-radius: 0px 4px 4px 0px; } .pre2 { width: 94%; margin: 28px auto; background: #fbfbfbc9; padding: 10px 20px 20px 20px; list-style-position: inside; box-shadow: 3px 3px 0px 0px #00000024; list-style: none; border-top: 3px solid #00000024; border-left: 3px solid #00000024; border-radius: 0px; position:relative; display: table; } .pre2:after { position: absolute; right: -12px; top: 50%; content: ''; background: #337ab7; width: 10px; height: 400px; transform: translate(0,-50%); border-radius: 0px 4px 4px 0px; } .pre2:before { position: absolute; left: -10px; top: 50%; content: ''; background: #337ab7; width: 10px; height: 400px; transform: translate(0,-50%); border-radius: 4px 0px 0px 4px; } .pre2 ul{ width: 100%; box-shadow: none; margin: 0px; padding: 0px; border-top: 0px; border-left:0px; } .pre2 ul li{ font-size: 13px; padding: 0px 20px; border-left: 0px; border-bottom: 0px; margin-bottom: 0px; position: relative; border-left: solid 2px #ab2927; color:#444; } .pre2 ul li a{ font-size: 13px; color: #444; border-bottom: 0px !important; } .pre2 ul li:after { position: absolute; left: 0px; top: 44%; content: ''; background: #ab2927; width: 16px; height: 1px; transform: translate(0,-50%); } .pre2 ul li:before { content: none!important; } .pre2 h3 { background: linear-gradient(135deg,rgba(82,62,232,.92),rgba(0,220,175,.92)); background-size: cover; border-radius: 0px; margin-top: -30px; padding: 64px 0px; font-size: 40px; color: #ffffff; text-align: center; } .pre2 h4:before { color: #001e30; content: "\21FE"; display: inline-block; font-family: 'ionicons'; margin-left: -24px; width: 24px; font-weight: bold; } .pre2 ul li a { color: #000204; border-bottom: none; } .pre2 ul { list-style: none; } .pre2 ul li{ padding-bottom: 4px;} .pre2 h3 a{ border-bottom:none; color: #ffffff6b;} /*.pre2 h3 { text-align: center; margin: 0px; padding: 10px; background: #337ab7 ;border-radius: 10px 10px 0 0; } /*.pre2 { background: #f7f7f7; border:none ; padding: 0px 0px 5px 0px; border-radius: 10px; box-shadow: 4px 5px 0px #337ab7; }*/ .trend-course .card-hover { display: flex; align-items: initial; justify-content: left; width: 100%; padding: 4px; box-shadow: 0px 0px 6px 0px #dedede; transition: all 0.5s; margin-bottom: 4px; background: #fff; overflow: hidden; position: relative; } /**.card-hover:hover { padding: 10px 0px 10px 10px; background: #f7f7f7; }*/ .trend-course .supcours-hov { position: absolute; top: 0px; left: 50%; padding: 6px 26px; background: linear-gradient(135deg, rgba(82, 62, 232, .92), rgba(0, 220, 175, .92)); height: 100%; opacity: 0; -webkit-transition: all 0.5s, -webkit-transform 0.5s; transition: all 0.5s, transform 0.5s; width: 100%; padding: 5px; } .trend-course .card-hover:hover .supcours-hov { opacity: 1; display: inline-block; -webkit-transition: all 0.5s, -webkit-transform 0.5s; transition: all 0.5s, transform 0.5s; width: 100%; height: 100%; opacity: 0.99; top: 0; left: 0; } .trend-course .card-hover p.btn-cour a { color: #fff; } .trend-course .courseinfo ul.Real { margin: 0px; padding: 0px 14px; } .trend-course .courseinfo { padding: 0px 0px 0px 10px; text-align: left; } .trend-course .courseinfo ul.Real li { color: #000; font-size: 10px; line-height: 14px; padding: 0px; } .trend-course .hovview p.cont1 { font-size: 10px; text-align: center; line-height: 20px; color: #ffd04b; } .trend-course .card-hover p.btn-cour { padding: 0px; border: 1px solid #fff; font-size: 12px; line-height: 21px; width: 98px; background: transparent; color: #fff; transform: translate(-50%, -50%); margin-bottom: 0px; left: 50%; top: 50%; position: absolute; float: left; } .trend-course .hovview { width: 100%; position: relative; float: left; display: flex; padding: 7px 0px; } .trend-course .whtpprpost { margin-bottom: 20px; } .trend-course .supcours-hov p.cont.mb0.white { margin-top: 10px; } .trend-course .section.section5 .card-hover:hover { padding: 10px 4px; } /* End 23-9-2019 Blogs Css */ @media screen and (max-width:320px) { } @media screen and (max-width:480px) { .pre1 ul { padding: 40px 10px 30px 48px; } .pre2 h3 { padding: 14px 0px; font-size: 20px; } .pre2 h4 { text-align: left; font-size: 16px; margin-left: 4px; line-height: 20px; } .pre1:after { position: absolute; left: 50%; content: ''; background: #337ab7; width: 80%; height: 11px; transform: translate(-50%,0); border-radius: 0px 0px 4px 4px; bottom: -7px; top: initial; } .pre1 { width: 100%; padding: 0px!important; } .pre1 h4 { font-size: 13px; width: 264px; text-align: center; } .pre1 ul:after { background:Transparent; } .pre1 ul { width: 100%; padding: 40px 10px 30px 28px; margin: 14px auto 0 auto; display: table; } .pre2 { width: 100%; padding: 10px 10px 20px 10px; } } @media screen and (max-width:767px) { .trend-course .hovview { padding: 0px 0px; } .trend-course .courseinfo ul.Real { margin: 0px; padding: 0px 7px; } .mob-trend { padding: 8px 0px; max-height: 401px; white-space: nowrap; overflow-y: scroll; } .ctmn3 { width: 98%; display: inline-block; padding: 6px 0; margin: 0px auto; } .browsecate ul li { font-size: 12px; padding: 4px 6px; margin-top: 2px; margin-bottom: 2px; } } @media (min-width:600px) and (max-width:600px) { .pre2 ul li a { font-size: 15px; } .pre2 h3 { padding: 14px 0px; font-size: 28px; } .mob-trend { max-height: 480px; } .trend-course .hovview img { width: 90px; } .pre1 h4 { width: 76%; text-align: center; } .pre1 ul:after { left: -70px; top: 42px; width: 40%; } .callto { width: 40%; float: right; position: absolute; right: 0px; top: 21px; } .trend-course .supcours-hov p.cont.mb0.white { margin-top: 22px; font-size: 18px; } .trend-course .hovview p.cont1 { font-size: 12px; } } @media (min-width:768px) and (max-width:991px) { .pre2 ul li a { font-size: 15px; line-height: 24px; } .trend-course .hovview img { width: 90px; } .trend-course .supcours-hov p.cont.mb0.white { margin-top: 22px; font-size: 18px; } .trend-course .hovview p.cont1 { font-size: 12px; } .trend-course .courseinfo ul.Real li { color: #000; font-size: 14px; line-height: 19px; padding: 0px; } .trend-course .courseinfo p.cont.mb0.dark { font-size: 19px; font-weight: 600; } .pre1 ul:after { width: 32%; top: 44px; } .pre1 ul { padding: 40px 10px 30px 44px; } .pre1 h4 { width: 64%; text-align: center; } } @media (min-width:992px) and (max-width:1024px) { .rght{ display:none; } .pre1 h4 { width: 64%; text-align: center; } .pre1 ul:after { top: 44px; } .pre1 ul { padding: 40px 10px 30px 40px; } .postbxful { width: 100%; } } @media (min-width:1025px) and (max-width:1200px) { } @media (min-width:1201px) and (max-width:1280px) { .pre1 ul:after { width: 25%; top: 44px; } .pre1 ul { padding: 40px 10px 30px 40px; } } @media (min-width:1366px) and (max-width:1366px) { .trend-course .courseinfo ul.Real li { font-size: 12px; line-height: 15px;; } } @media (min-width:1440px) and (max-width:1440px) { .trend-course .courseinfo ul.Real li { font-size: 12px; line-height: 15px;; } } @media (min-width:1600px) and (max-width:1680px) { .pre2 ul li a { font-size: 15px; line-height: 24px; } .trend-course .courseinfo ul.Real li { font-size: 12px; line-height: 15px;; } } @media screen and (min-width:1601px) { .pre2 ul li a { font-size: 15px; line-height: 24px; } .trend-course .courseinfo ul.Real li { font-size: 12px; line-height: 15px;; } } @media (min-width:1920px) and (max-width:1920px) { .pre1 ul:after { left: -110px; } .pre1 ul li a { font-size: 18px; } .pre1 ul li ul li a { font-size: 15px; line-height: 25px; } .pre2 h4 { font-size: 1em!important; } .pre2 ul li a { font-size: 17px; line-height: 24px; } } @charset "utf-8";.sti{position:relative;display:inline-block}.sti .sti_reset{bottom:auto !important;display:inline-block !important;float:none !important;left:auto !important;margin:0 !important;position:relative !important;right:auto !important;top:auto !important}.sti .sti-share-box{position:absolute;z-index:999;display:block}.sti .sti-share-box .sti-btn{display:block;position:relative;cursor:pointer;-webkit-transition:all 0s linear;-moz-transition:all 0s linear;-ms-transition:all 0s linear;-o-transition:all 0s linear;transition:all 0s linear}.sti .sti-mobile-btn{position:absolute;z-index:999;display:block;cursor:pointer;width:36px;height:36px;background:#000;fill:#fff}.sti .sti-mobile-btn svg{width:24px;height:24px;margin:0;vertical-align:middle;text-align:center;display:block;position:absolute;left:50%;top:50%;margin-top:-12px;margin-left:-12px}.sti.sti-mobile .sti-share-box{display:none}.sti.sti-mobile.sti-mobile-show .sti-share-box{display:block}.sti.sti-mobile.sti-mobile-show .sti-mobile-btn{display:none}.sti .sti-link-form{width:400px;border:1px solid #aaa;background:#f4f4f4;position:absolute;border-radius:4px;top:0;left:100%;padding:2px;margin:0;margin-left:5px;font-size:14px;vertical-align:baseline}.sti .sti-link-form .sti-link-label{display:none}.sti .sti-link-form .sti-link-input{-webkit-appearance:none;border-radius:0;font:inherit;position:relative;display:block;overflow:visible;margin:0 !important;background:#fff !important;font-size:14px !important;line-height:18px !important;padding:6px !important;border:1px solid rgba(0,0,0,.2) !important;width:386px !important}.sti .sti-link-form .sti-link-input:focus{outline:none}.sti.horizontal .sti-link-form{top:110%;left:0;margin-left:0}.sti .sti-facebook-btn{background-color:#3b5998}.sti .sti-facebook-btn:hover{background-color:#2d4373}.sti .sti-twitter-btn{background-color:#55acee}.sti .sti-twitter-btn:hover{background-color:#2795e9}.sti .sti-google-btn{background-color:#dd4b39}.sti .sti-google-btn:hover{background-color:#c23321}.sti .sti-linkedin-btn{background-color:#0077b5}.sti .sti-linkedin-btn:hover{background-color:#046293}.sti .sti-pinterest-btn{background-color:#ec1a22}.sti .sti-pinterest-btn:hover{background-color:#d4171e}.sti .sti-tumblr-btn{background-color:#35465c}.sti .sti-tumblr-btn:hover{background-color:#222d3c}.sti .sti-reddit-btn{background-color:#5f99cf}.sti .sti-reddit-btn:hover{background-color:#3a80c1}.sti .sti-digg-btn{background-color:#303030}.sti .sti-digg-btn:hover{background-color:#171717}.sti .sti-delicious-btn{background-color:#4576bd}.sti .sti-delicious-btn:hover{background-color:#3c67a3}.sti .sti-vkontakte-btn{background-color:#507299}.sti .sti-vkontakte-btn:hover{background-color:#43648c}.sti .sti-odnoklassniki-btn{background-color:#f60}.sti .sti-odnoklassniki-btn:hover{background-color:#e55c00}.sti .sti-link-btn{background-color:#0f65ef}.sti .sti-link-btn:hover,.sti .sti-link-btn.active{background-color:#0c51bf}.sti .sti-email-btn{background-color:#777}.sti .sti-email-btn:hover{background-color:#5e5e5e}.sti .sti-share-box .sti-btn{fill:#fff;position:relative}.sti .sti-share-box .sti-btn svg{margin:0;vertical-align:middle;text-align:center;display:block;position:absolute;left:50%;top:50%}.sti.style-flat .sti-share-box .sti-btn{width:48px;height:48px}.sti.style-flat .sti-share-box .sti-btn svg{width:24px;height:24px;margin-top:-12px;margin-left:-12px}.sti.style-flat .sti-share-box .sti-btn.sti-digg-btn svg{width:26px;height:26px;margin-top:-13px;margin-left:-13px}.sti.style-flat-small .sti-share-box .sti-btn{width:36px;height:36px}.sti.style-flat-small .sti-share-box .sti-btn svg{width:16px;height:16px;margin-top:-8px;margin-left:-8px}.sti.style-flat-small .sti-share-box .sti-btn.sti-digg-btn svg{width:18px;height:18px;margin-top:-9px;margin-left:-9px}.sti.style-box .sti-share-box{width:38px;background-color:#fafafa;background-color:rgba(250,250,250,.8);padding:4px 0;border-radius:10px;-webkit-box-shadow:#ccc 0px 0px 3px 0px;-moz-box-shadow:#ccc 0px 0px 3px 0px;box-shadow:#ccc 0px 0px 3px 0px}.sti.style-box .sti-share-box .sti-btn{width:24px;height:24px;margin:4px auto;border-radius:2px}.sti.style-box .sti-share-box .sti-btn:hover{opacity:.7}.sti.style-box .sti-share-box .sti-btn svg{width:14px;height:14px;margin-top:-7px;margin-left:-7px}.sti.style-box .sti-share-box .sti-btn.sti-digg-btn svg{width:18px;height:18px;margin-top:-9px;margin-left:-9px}.sti.style-circle .sti-share-box .sti-btn{width:36px;height:36px;border-radius:50%;margin-bottom:1px;box-shadow:0 1px 4px rgba(0,0,0,.2)}.sti.style-circle .sti-share-box .sti-btn svg{width:16px;height:16px;margin-top:-8px;margin-left:-8px}.sti.style-circle .sti-share-box .sti-btn.sti-digg-btn svg{width:18px;height:18px;margin-top:-9px;margin-left:-9px}.sti.style-square .sti-share-box .sti-btn{width:24px;height:24px;border-radius:5px;margin-bottom:2px}.sti.style-square .sti-share-box .sti-btn svg{width:14px;height:14px;margin-top:-7px;margin-left:-7px}.sti.style-square .sti-share-box .sti-btn.sti-digg-btn svg{width:16px;height:16px;margin-top:-8px;margin-left:-8px}.sti.horizontal .sti-share-box .sti-btn{display:inline-block;vertical-align:top}.sti.style-box.horizontal .sti-share-box{width:auto;padding:5px}.sti.style-box.horizontal .sti-share-box .sti-btn{display:inline-block;margin:1px 3px}.sti.style-circle.horizontal .sti-share-box .sti-btn{margin-bottom:0;margin-right:1px}.sti.style-square.horizontal .sti-share-box .sti-btn{margin-bottom:0;margin-right:2px} .blogdtlright .cta-inln {background: linear-gradient(45deg, #E91E63, #3F51B5) !important; padding: 0;} .cta-inln1 { background: linear-gradient(to right,#343d9c,#32c2d2) !important; padding: 0; } .cta-inln2 { background: linear-gradient(45deg, #9C27B0, #142ba9) !important; padding: 0; } .cta-inln3 { background: linear-gradient(45deg, #2196F3, #4CAF50) !important; padding: 0; } .wqqes img { width: 86%; float: right; } /******************************************************/ #style-2::-webkit-scrollbar-track{ -webkit-box-shadow: inset 0 0 6px rgba(0,0,0,0.3); border-radius: 10px; background-color: #F5F5F5; } #style-2::-webkit-scrollbar{ width: 6px; background-color: #F5F5F5; } #style-2::-webkit-scrollbar-thumb{ border-radius: 10px; -webkit-box-shadow: inset 0 0 6px rgba(0,0,0,.3); background-color: #555; } .temp-2-custom-bx .affix { position: fixed !important; top: 110px !important; width: 223.73px; margin: 0; box-shadow: none !important; } .pre23 { background: transparent !important; display: block; float: left; padding: 0 !important; border: 1px solid #e8e8e8; border-bottom: 4px solid #1289ee; } .scroll-x { padding: 0; height: 74vh; overflow:auto; box-shadow: none; } /*/*//*/ add By N 06-10-2021*/ #style-2 ul{ list-style: none; margin: 0; padding: 0; } #style-2 ul li a { text-align: left; text-decoration: none; } #style-2 .card-header2 ul { padding: 0 0px 0px 23px; list-style: circle; } /*.accordion.scroll-x button { padding: 10px 8px; color: #323232; font-size: 13px; line-height: 18px; font-weight: 500; text-decoration: none; display: block; border-left: 2px solid transparent; }*/ /*/*//*/ add By N 06-10-2021*/ .scroll-x li a { padding: 10px 8px; color: #323232; font-size: 13px; line-height: 18px; font-weight: 500; text-decoration: none; display: block; border-left: 3.7px solid transparent; } .scroll-x li { position: relative; background: #fff; font-size: 13px; border-bottom: 1px solid #EEEEEE; font-weight: 500; } .scroll-x li:hover { background: #f4f4f4; } .temp-2-custom-bx .active { color: white; background-color: #f4f4f4; color: #323232; border-left: 2px solid #3446a0; } h4.inner-scroll-x { text-align: center; padding: 10px 10px; background: linear-gradient(to right,#343d9c,#32c2d2); color: white; margin: 0; font-size: 18px; } /*Right SideBar*/ .rghtsideblg-new-x p { margin: 0; } .rghtsideblg-new-x p { position: relative; background: #fff; font-size: 13px; border-bottom: 1px solid #EEEEEE; font-weight: 500; border-left: 2px solid transparent; transition: 0.3s; } .rghtsideblg-new-x p a { padding: 10px 8px; color: #23527c; font-size: 13px; line-height: 18px; font-weight: 500; text-decoration: none; display: block; } .rghtsideblg-new-x { background: transparent !important; display: block; float: left; padding: 0 !important; border: 1px solid #e8e8e8; /* border-bottom: 4px solid #1289ee; */ overflow: auto; margin-bottom: 25px; } .rghtsideblg-new-x p:hover { background: #f4f4f4; border-left: 2px solid #3446a0; transition: 0.3s; } .rght-new-x .lead1{ font-size: 1em; padding-left: 1.7em; margin-bottom: 10px; } .rght-new-x .lead1 { font-size: 1em; margin-bottom: 0; background: linear-gradient(to right,#343d9c,#32c2d2); padding: 8px 23px; color: white; } .rght-new-x.sticky { width: 223px!important; padding: 0 !important; } .affix .rght-new-x2, .affix .rght-new-x3{ display: none; } .temp-2-custom-bx .rght { background: #ffffff; padding: 20px 14px; box-shadow: none; width: 100%; border: 1px solid #e8e8e8; border-bottom: 4px solid #1a70b9; } .temp-2-custom-bx #email-error, #name-error, #mobile-error { color: #ab2927; text-align: left; background: #fbfbfb; font-size: .6em; line-height: normal; padding: 0 0; margin-top: 8px; font-weight: 500; float: left; } .temp-2-custom-bx .getcall-box { padding: 0; width: 100%; } .temp-2-custom-bx button.buttonctadarkbtn.btn { font-size: 13px; padding: 4px 0; } .temp-2-custom-bx .lead5 span{ font-size:1.3em; } .col-centered { float: none; margin: 0 auto; } .carousel-control { width: 8%; width: 0px; } .carousel-control.left, .carousel-control.right { margin-right: 40px; margin-left: 32px; background-image: none; opacity: 1; } .carousel-control > a > span { color: white; font-size: 29px !important; } .carousel-col { position: relative; min-height: 1px; padding: 5px; float: left; } .active > div { display:none; } .active > div:first-child { display:block; } /*xs*/ @media (max-width: 767px) { .carousel-inner .active.left { left: -50%; } .carousel-inner .active.right { left: 50%; } .carousel-inner .next { left: 50%; } .carousel-inner .prev { left: -50%; } .carousel-col { width: 50%; } .active > div:first-child + div { display:block; } } /*sm*/ @media (min-width: 768px) and (max-width: 991px) { .carousel-inner .active.left { left: -50%; } .carousel-inner .active.right { left: 50%; } .carousel-inner .next { left: 50%; } .carousel-inner .prev { left: -50%; } .carousel-col { width: 50%; } .active > div:first-child + div { display:block; } } /*md*/ @media (min-width: 992px) and (max-width: 1199px) { .carousel-inner .active.left { left: -33%; } .carousel-inner .active.right { left: 33%; } .carousel-inner .next { left: 33%; } .carousel-inner .prev { left: -33%; } .carousel-col { width: 33%; } .active > div:first-child + div { display:block; } .active > div:first-child + div + div { display:block; } } /*lg*/ @media (min-width: 1200px) { .carousel-inner .active.left { left: -25%; } .carousel-inner .active.right{ left: 25%; } .carousel-inner .next { left: 25%; } .carousel-inner .prev { left: -25%; } .carousel-col { width: 25%; } .active > div:first-child + div { display:block; } .active > div:first-child + div + div { display:block; } .active > div:first-child + div + div + div { display:block; } } .block { width: 306px; height: 230px; } .glyphicon-chevron-right:before { content: ">" !important; display: table; font-family: cursive; width: 30px; height: 30px; line-height: 25px; background: #34449f85; border-radius: 20px; } .glyphicon-chevron-left:before { content: ">" !important; transform: rotate( 180deg); display: table; font-family: cursive; width: 30px; height: 30px; line-height: 25px; background: #34449f85; border-radius: 20px; } .Interview-Questions h4 { margin: 0; background: white; padding: 15px 15px; border-bottom: 2px solid #113f7b; font-size: 14px; line-height: 20px; color: black; } /* .row.trend-course.Interview-Questions img { min-height: 120px; } */ .wqqes img { width: 86%; float: right; } .thumbview img.img-responsive { width: 16px; display: inline-block; } .comment_dtl li ul li:after{ display: none; } .comment_dtl li ul li .sed { width: 42px; height: 42px; line-height: 42px; font-size: 22px; margin-top: 10px; } .comment_dtl ul li ul li .sedtxt { border:none !important; } Just a moment...
Just a moment...

Grab Deal : Upto 30% off on live classes + 2 free self-paced courses - SCHEDULE CALL

- Data Science Blogs -

How Comparison of Two Populations Data look like?

Contents Index

Introduction

Comparison of two population-related data refers to the practice of finding the difference between two different population-related data created based on the same information. For example, if the data is based on the working time of the employee between the employee population of country 1 to that of the employee population of country 2. Another example could be the expenditure of population of location A compared to the expenditure of population of location B. In the latter case also, data is collected based on the expenditure of the population but of two different locations, i.e. A and B. This comparison can be either based on paired observation or independent observation or sample. These Independent observations are further divided into Large and Small observations.

Compare the Two Population Mean Using Paired Observation

To explain this, consider an example in which an oil and gas industry wants to compare the fuel economy obtained by two different types of gasoline. Since fuel economy varies from car to car, if we consider mean fuel economy of two independent observations of vehicles that run on the two types of fuel that were considered for comparison, this may arise difficulty in detecting the accurate result due to the large variability from vehicle to vehicle making any difference in the ultimate result, even if one type of gasoline is better than the other.

In such cases the more sensible step would be instead of taking an independent observation, one must select a pair of cars, where the first car in each pair works on type 1 gasoline while the second car operates on the type 2 gasoline.  Following table represents the same data of the different type of fuels used by the same car companies: 

Make and Model

Type 1 Fuel Car

Type 2 Fuel Car

Buick Lacrosse

17.0

17.0

Dodge Viper

13.2

12.9

Honda CR-Z

35.3

35.4

Hummer H 3

13.6

13.2

Lexus RX

Read: Learn The Critical Data Mining Techniques

32.7

32.5

Mazda CX-9

18.4

18.1

Saab 9-3

22.5

22.5

Toyota Corolla

26.8

26.7

Volvo XC 90

15.1

15.0

It would not be correct to analyze the data using normal formulas. For these types of samples, that is paired samples, one should calculate the difference in the numbers in each pair to obtain a column of numbers and treat this list of difference as the actual data to be analyzed. While computing the difference, one should keep in mind that it does not matter in what order subtraction is done, but the same order must be followed for all the data, e.g., if subtraction is done in the order such that, (type1_gasoline) – (type2_gasoline) for the first data, then for all the data same subtraction formula must be followed.

Due to the same reason, there may be both negative as well as positive values. This new may be considered as a random sample of the same number of elements as in actual sample i.e. n = 9 with mean,

µ diff   = µtype1 - µtype2

This approach converts the paired two-sample problem into a one-sample problem.

Test the Difference of Two Population Mean Using Independent Sample

To explain this concept, it would be quite good to take help from an example. Consider a case in which comparison is made between two groups of students at a local high school on the math portion. The groups were divided into, group 1 consist of 100 students those who are in the accelerated program and group 2 consist of 100 students those who study in traditional format program. So, the problem to solve is that does the student studying in accelerated program score higher in mathematics than those who study in traditional format program? To test this claim, a test was performed.

Read: Data Science vs Software Engineering - What you should know?

After evaluation of the test, the student of the accelerated program had an average score of 590 with a standard deviation of 50 and the student in the traditional format program had an average of 520 with a standard deviation of 75 in the mathematics subject. For this comparison, the level of significance is taken as 1%. For this case, we are comparing the two suggestions whose samples are independent, due to the fact scholars in the extended program are one of a kind from those of traditional layout programs and are not dependent on each other. So,

Step 1:  is to identify the hypothesis

H0 : µ1 = µ2 (here we are assuming that there is no difference between the two   groups)

For the alternative hypothesis,

HA: µ1 > µ2 (we're the usage of greater than because we want to understand that the pupil inside the accelerated program have a higher score than their other comrades in math's subject) 

Step 2: Identify the level of significance

α = 0.01, given

Step 3: It consists of computation. 

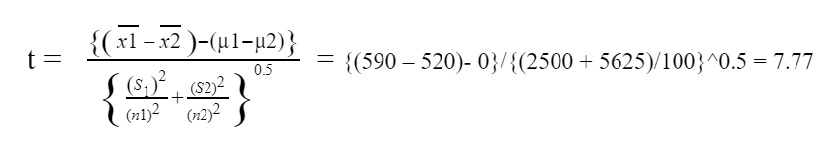
Step 4: Compute critical value. Since this test follows a t distribution, we are going to use t-table


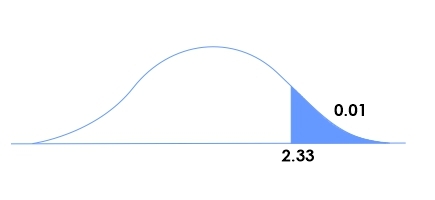
Figure 1         

Df = Smaller of n1-1 or n2-1 = 99                                                                               

Looking into the t-table and locating 99 degrees of freedom, we got to know that Critical value is 2.33

Step 5:  Reject speculation H0, there may be sufficient evidence to suggest that the students reading in increased software at a local excessive school have better rankings in mathematics issues than their comrades in Traditional layout programs.

Test the Difference of Two Population Proportion Using Independent Sample

Figure 2

Above mentioned formula is used in testing the difference of two population proportions using an independent sample. The test statistic has the usual everyday distribution. Each sample has to be large and each of the intervals has to lie inside [0, 1]. Let's look at the following example to perform the check 

A permit to work on a residential project is issued to general contractors by the department of code enforcement of a county government. The result is inspected by the department which allows "pass" or "fail" certification, for each permit issued. Re-inspection of the failed permit maintains until it gets a bypass certificate. Since the department got frustrated by the high cost of re-inspection, it decided to publish the inspection record of all contractors on the web. It turned into the hope that public get entry to the statistics would lower the re-inspection fee. A year after the web access was made public, two samples of information were randomly decided on. One pattern became determined from the pool of records earlier than the netbook and one after. The proportion of initiatives that handed on the primary inspection turned into states for each sample. The outcomes are summarized under.

Construct a point estimate and a 90% self-belief c program language period for the difference in the passing fee on the first inspection among the 2 time periods. Now, test whether there is adequate proof to infer that open web access to the review records has expanded the proportion of ventures that passed on the principal assessment by over 5% points. Consider the critical value methodology at the 10% level of significance.

Read: An Easy Way to Understand Adaboost

Solution:

Step 1: Considering the naming of the populations an expansion in the passing rate at the main investigation by more than 5 % points after community on the web might be told as p1 <p2- 0.05, which through algebra is equivalent to p1 − p2 < − 0.05. Since the null hypothesis is continuously communicated as a correspondence, with the equal quantity at the privilege as is in the alternative speculation, the test is

H0 : p1 − p2 = − 0.05 vs. Ha : p1 − p2 < − 0.05 @ α = 0.10

Step 2: Since the test is as for a distinction in populations proportions the test measurement is given in Figure 3

Figure 3

Step 3: Inserting the values given in example and the value D0 = − 0.05 into the method for the check statistic gives value in the following given Figure 4

Figure 4

Step 4: Since the symbol in Ha is “<” this is a left-tailed test, so there is a single critical value, zα = − z0.10. From the last row in Figure 7.1.6 z0.10 = 1.282, so −z0.10 = − 1.282. The rejection region is (− ∞, − 1.282].

Step 5: As shown in Figure 5 the check statistic falls in the rejection region. The selection is to reject H0. In the context of the hassle our conclusion is:

The facts provide enough proof, at the 10% stage of significance, to conclude that the rate of passing on the primary inspection has accelerated through extra than 5 percentage points because records have been publicly published at the web.

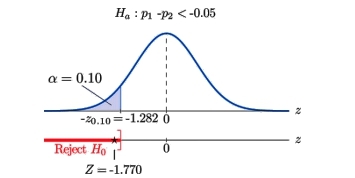
Figure 5
 

Conclusion

A point estimate for the difference in population means is honestly the distinction within the corresponding sample method. In the context of estimating or trying out hypotheses concerning population means, "huge" samples approach that each sample is massive. A self-assurance c programming language for the difference in population means is computed the usage of a formulation inside the same style as became accomplished for a single population suggest. The most effective difference is in the method for the standardized take a look at the statistic.

When the statistics are collected in pairs, the variations computed for every pair are the data which are used within the formulation.

The identical five-step method used to check hypotheses concerning an unmarried population proportion is used to test hypotheses concerning the difference among population proportions. The simplest difference is within the formula for the standardized test statistic.

Please leave the query and comments in the comment section.

Read: What Qualifications Are Required To Become Data Scientist?


Data Science Tutorial Overview

Introduction

Careers

Data Science Vs. Different Technologies

Tools

Useful Resources

Interview

fbicons FaceBook twitterTwitter lingedinLinkedIn pinterest Pinterest emailEmail

    Logo

    JanBask Training Team

    The JanBask Training Team includes certified professionals and expert writers dedicated to helping learners navigate their career journeys in QA, Cybersecurity, Salesforce, and more. Each article is carefully researched and reviewed to ensure quality and relevance.

Comments

Trending Courses

Cyber Security Course

Cyber Security

  • Introduction to cybersecurity
  • Cryptography and Secure Communication 
  • Cloud Computing Architectural Framework
  • Security Architectures and Models
Cyber Security Course

Upcoming Class

17 days 03 Oct 2025

View Details
QA Course

QA

  • Introduction and Software Testing
  • Software Test Life Cycle
  • Automation Testing and API Testing
  • Selenium framework development using Testing
QA Course

Upcoming Class

6 days 22 Sep 2025

View Details
Salesforce Course

Salesforce

  • Salesforce Configuration Introduction
  • Security & Automation Process
  • Sales & Service Cloud
  • Apex Programming, SOQL & SOSL
Salesforce Course

Upcoming Class

3 days 19 Sep 2025

View Details
Business Analyst Course

Business Analyst

  • BA & Stakeholders Overview
  • BPMN, Requirement Elicitation
  • BA Tools & Design Documents
  • Enterprise Analysis, Agile & Scrum
Business Analyst Course

Upcoming Class

3 days 19 Sep 2025

View Details
MS SQL Server Course

MS SQL Server

  • Introduction & Database Query
  • Programming, Indexes & System Functions
  • SSIS Package Development Procedures
  • SSRS Report Design
MS SQL Server Course

Upcoming Class

3 days 19 Sep 2025

View Details
Data Science Course

Data Science

  • Data Science Introduction
  • Hadoop and Spark Overview
  • Python & Intro to R Programming
  • Machine Learning
Data Science Course

Upcoming Class

10 days 26 Sep 2025

View Details
DevOps Course

DevOps

  • Intro to DevOps
  • GIT and Maven
  • Jenkins & Ansible
  • Docker and Cloud Computing
DevOps Course

Upcoming Class

1 day 17 Sep 2025

View Details
Hadoop Course

Hadoop

  • Architecture, HDFS & MapReduce
  • Unix Shell & Apache Pig Installation
  • HIVE Installation & User-Defined Functions
  • SQOOP & Hbase Installation
Hadoop Course

Upcoming Class

10 days 26 Sep 2025

View Details
Python Course

Python

  • Features of Python
  • Python Editors and IDEs
  • Data types and Variables
  • Python File Operation
Python Course

Upcoming Class

4 days 20 Sep 2025

View Details
Artificial Intelligence Course

Artificial Intelligence

  • Components of AI
  • Categories of Machine Learning
  • Recurrent Neural Networks
  • Recurrent Neural Networks
Artificial Intelligence Course

Upcoming Class

18 days 04 Oct 2025

View Details
Machine Learning Course

Machine Learning

  • Introduction to Machine Learning & Python
  • Machine Learning: Supervised Learning
  • Machine Learning: Unsupervised Learning
Machine Learning Course

Upcoming Class

31 days 17 Oct 2025

View Details
Tableau Course

Tableau

  • Introduction to Tableau Desktop
  • Data Transformation Methods
  • Configuring tableau server
  • Integration with R & Hadoop
Tableau Course

Upcoming Class

10 days 26 Sep 2025

View Details

Browse Categories

Search Posts

Reset

Related Posts

What is Hypothesis Testing | Steps, Types, and Applications   eye-dark 993

How Online Training is Better Than In-Person Training?   eye-dark 163k

The Battle Between R and Python   eye-dark 4.4k

How to Do Data Manipulation of Packages Using R?   eye-dark 5.6k

What Is Time Series Modeling? Forecasting Process and Model   eye-dark 6k

Receive Latest Materials and Offers on Data Science Course

Online Course

Tutorials

Salesforce Tutorial

Software Testing Tutorial

SQL Tutorial

Business Analyst Tutorial

Devops Tutorial

Data Science Tutorial

AWS Tutorial

Hadoop Tutorial

SSRS Tutorial

AWS S3 Tutorial

Functional Testing Tutorial

SSAS Tutorial

Automation Testing Tutorial

Manual Testing Tutorial

Selenium Tutorial

Kubernetes Tutorial

Scala Tutorial

ETL Testing Tutorial

Python Tutorial

Pyspark Tutorial

R Tutorial

Unit Testing Tutorial

API Testing Tutorial

Puppet Tutorial

Integration Testing Tutorial

Chef Tutorial

Jenkins Tutorial

Ansible Tutorial

Vagrant Tutorial

Docker Tutorial

Interviews