Jan 23, 2020 
4.2k
06
DecBlack Friday Deal : Up to 40% OFF! + 2 free self-paced courses + Free Ebook - SCHEDULE CALL
- Data Science Blogs -
In the domain of data science, most of the models being built are usually classification model. Reason for the same being that most of the time we are trying to recommend stuff or place a new entry in it’s more legit place. This happens in real word more as compared to forecasting something. Thus, it remains the same for the domain of artificial intelligence. In this blog, a classification algorithm named as K-nearest neighbor is being discussed.
K-nearest neighbor is a typical example of a non-parametric classification and regression model. Primarily, it had found more use as a classification technique as compared to regression. Whatever the use may be, the input for this algorithm consists of training samples from the feature space. The output is specified for training varies as to whether it is being used for classification or regression. In the case of classification, the output is the class membership whereas in regression, the output is the value.
K-nearest neighbor is a lazy learner i.e. it delays the classification until a query is made. K-nearest neighbor is a type of supervised learner stating this we mean that the dataset is prepared as (x, y) where x happens to be the input vector and y is the output class or value as per the case.
It also belongs to a type of learning known as instance-based learning which is also called non-generalizing learning. This is so because K-nearest neighbor never constructs any weight matrix or internal model but it only keeps instances of the training data with it. Classification in algorithms with instance-based learning is done by simply using the majority vote of the nearest neighbors. In other words, the query instance is assigned the class whose most components are found in its vicinity.
To check for the components in the vicinity, various mathematical models known as distances are used. Actually, when we query the K nearest neighbor for any new data point, it calculates the distance of each training point from the new point. This computation of distance is done primarily using Euclidian distance but there are other methods as well which are stated below:
1). Euclidean Distance:
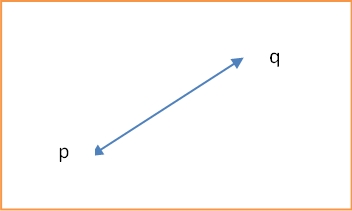
The Euclidean distance the length of the ordinary straight line between two points as shown in the figure below. Mathematically,
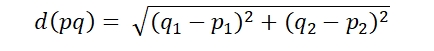
For n points gr
Read: SQL- A Leading Language for Data Science Experts
2). Manhattan Distance:
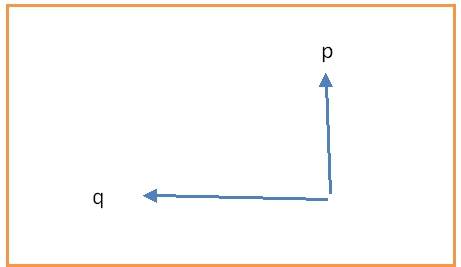
Unlike Euclidean distance, which is a point-to-point line segment, Manhattan distance also points to point but not through a line segment. It follows a type of geometry known as taxicab geometry. This term, Manhattan distance originated from the grid layout in the Manhattan island where the shortest path between two points is through the intersection. A Manhattan distance between two points looks as shown in the figure below:
Mathematically,
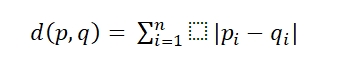
Where d(p,q) is the distance between p and q
3). Hamming Distance:
This is used when under consideration variables are categorical. Hamming distance is defined as
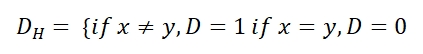
The next step is to measure the distance of the point from the points in the training data set. Once this is done, we pick the closest point. The number of points at any point under consideration defines the value of k.
Till this point in this blog, we are discussing the k-nearest neighbor and have over and again stated that the choice K remains an important parameter in finding the optimum K as it can have diverse effects on the classifier. As we know that in all the machine learning algorithms there is a hyperparameter that is chosen by the architect of the algorithm to make the best fit. In the case of K-nearest neighbor, the K controls the shape of the decision boundary. Being a hyperparameter to be chosen by the architect, the range of K lies from [0,∞]. This leads to a scenario where most of the time, global maxima is neither important nor viable to find.
Read: How to Do Data Manipulation of Packages Using R?
Adding to this, if k is too small, the classifier will be limited in its classification power and will overlook the overall distribution of the inheriting dataset. In other words, a small value of K goes for a more flexible approach that decreases the bias and introduces high variance. The other side of this approach is that if the value of k is large the decision boundary will be much more smooth that will introduce smoother boundaries with low variance and increased bias.
Designing a K-nearest neighbor based classifier is can be done by using a number of libraries available. In this example, sklearn is utilized for training the k-nearest neighbor and matplotlib is used for plotting the decision boundaries. Iris flower dataset which is provided in sklearn.datasets will be used for training and demonstration purposes. {IRIS flower dataset is a classical dataset detail about which can be found here.}
First, import all the libraries required as:
import numpy as np import matplotlib.pyplot as plt from matplotlib.colors import ListedColormap from sklearn import neighbors, datasets
Now, defining hyperparameter is important which can be done as
#k can be initialized/used as per the discretion. ( local minima k can be found using the elbow method. Here, we take a number of values for k and plot the accuracy for all of them. The point where we find a reduction in the value of accuracy, we assume that that’s a local maxima and stop there. IT shows up as a bent elbow on the graph. Hence, the name) K = 10
Load the dataset:
iris = datasets.load_iris()
Initialize the input vector and target values:
input_vector = iris.data[:, :2] target = iris.target
Define the step size:
Step = 0.3
Now, as this is a classifier whose hyper parameter named as k can vary, we’ll have to use decision boundaries with multiple colors for visualization purpose. So, Create the color maps:
cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue']) cmap_bold = ListedColormap(['darkorange', 'c', 'darkblue'])
Finally, train the classifier and plot the results as:
for weights in ['uniform', 'distance']:
clf = neighbors.KNeighborsClassifier(K, weights=weights)
clf.fit(input_vector, target)
# Assign color and plot the decision boundaries
input_vector_min, input_vector_max = input_vector[:, 0].min() - 1, input_vector[:, 0].max() + 1
target_min, target_max = input_vector[:, 1].min() - 1, input_vector[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(input_vector_min, input_vector_max, step),
np.arange(target_min, target_max, step))
predict = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Showing results in color plot
predict = predict.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# Plotting the training data points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = %i, weights = '%s')"
% (K, weights))
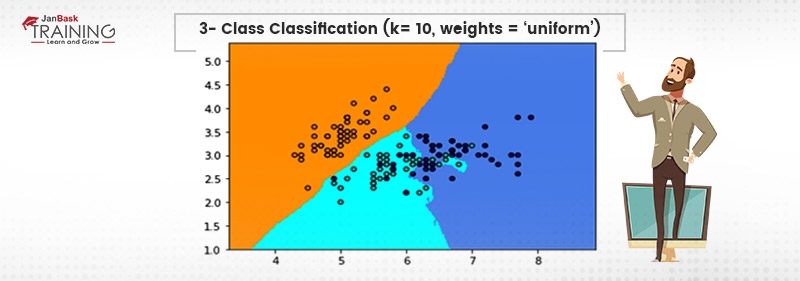
The output of the above will be shown as:
Read: Deep Learning Tutorial Guide for Beginners
We can visualize the decision boundaries of the classifier. The above code can be deployed using flask and other allied technologies. They can be queried as an API call or as per requirement.
Advantages:
The biggest advantage of k-nearest neighbor is that is quite simple to implement as well as understand. This algorithm takes an extremely small amount of time to implement and thus, can be used as an analysis tool for complex datasets. Also, the non-parametric nature of this algorithm gives it an advantage as compared to other parametric models.
Disadvantages:
As can be seen from the blog that k-nearest neighbor is extremely computationally expensive during its testing phase as it makes no weight matrix which makes it quite costly to use in a fast-moving industrial setting. Also, K-nearest neighbor will not work well in skewed class distribution.
Final Words:
K-nearest neighbor is an extremely simple and easy to understand algorithm with its uses in recommendation engines, client labeling, and allied stuff. In the above blog, we have gone through the KNN algorithm, its use as well as advantages and disadvantages. As can be seen, because of its inherent simplicity which comes at a cost of storage, the KNN is still widely used.
Please leave the query and comments in the comment section.
FaceBook
Twitter
LinkedIn
Pinterest
Email
A dynamic, highly professional, and a global online training course provider committed to propelling the next generation of technology learners with a whole new way of training experience.
Cyber Security
QA
Salesforce
Business Analyst
MS SQL Server
Data Science
DevOps
Hadoop
Python
Artificial Intelligence
Machine Learning
Tableau
Search Posts
Related Posts
Receive Latest Materials and Offers on Data Science Course
Interviews
Mar 06, 2024
632k
632k