Jan 24, 2020 
5.3k
03
JanChristmas Special : Upto 40% OFF! + 2 free courses - SCHEDULE CALL
- Data Science Blogs -
In this blog, we are going to discuss the theoretical concepts of logistic regression as well as the implementation of logistic regression using sklearn.
Logistic regression belongs to the category of classification algorithms and is precisely used to where the classes are a discrete set. Real-world use cases can be spam recognition, online fraud detection and allied. Basically, logistic regression performs a binary classification by utilizing a logistic sigmoidal function and returns a probability value.
Logistic regression is a classical model in the domain of statistics which is still in use. It differs from linear regression as it’s not used to make a forecast as the name suggests instead it's used for classification. A classical case for this would be a credit card default. In this case, the institution offering the card is only interested in the only wheatear the client would default on payment or not.
Now, this problem can be approached in broadly two ways. One is making the forecast of the client's earnings and making a decision based on financial status. Now, this model will be extremely complex as it has to go through forecasts for the economy, job growth and allied.
The other way around this problem is to use a model like logistic regression which will make the forecast based upon the probability of default by the client. Because of the basic nature of the probability, this model will return a value between 0 and 1. Depending upon the risk appetite of the issuing organization,we can label probability, say above 0.6 as default and rest as not default. So, if an applicant is having a score of say 0.40 then the model will predict it as ‘not default’. Logistic regression is actually an extension of linear regression for classification. As the domain of linear regression is [-∞, ∞], so, a sigmoidal function is used to restrict the domain. The sigmoidal function is defined as:
f(x)= 1/1+e^x
And its looks like an S-shaped curve as shown in the figure below:
Read: ARIMA like Time Series Models and Their Autocorrelation
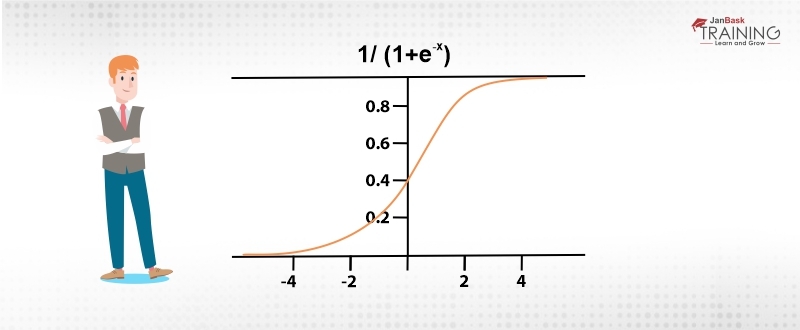
The sigmoidal function saturates any argument under consideration between the range of 0 and 1 which can be seen as highly likely or highly unlikely.
Maximum Likelihood estimation – the learning algorithm for Logistic regression:
The maximum-likelihood estimation algorithm is one of the most frequently used learning algorithms in the machine learning domain. This model makes an assumption about the coefficient and the best coefficient are those which will produce the result of highly likely as 1 and highly unlikely as 0. Though this rarely happens a value near to these is quite good. In general terms, the maximum-likelihood algorithm can be viewed as a search algorithm that tries to find out a value of coefficients which can minimize the error in the model.
In statistical theory, the maximum-likelihood algorithm maximizes the likelihood function. Depending upon the type of distribution the working of maximum-likelihood varies and can be thought of like a simple version of gradient descent. (Gradient descent is used for optimizing by reducing the gradient of step till a minimum value is reached.)
Implementing logistic regression varies to some extent on the use of the library as well as language. Here, logistic regression will be implemented using sklearn and python. Sklearn provides a few datasets for training purposes out of which the IRIS dataset is being used, in this example.
First, the libraries used in the process are imported:
from sklearn.datasets import load_iris import numpy as np import pandas as pd import matplotlib.pyplot as plt
Note: Iris dataset is a classical dataset and details about this dataset can be found here. Once the libraries are there, let’s check how their width and length look against each other.
Read: Difference Between Data Scientist and Data Analyst
X=load_iris().data Y=load_iris().target plt.figure()
Once, the data is in working memory, training the model is the first step. In the case of logistic regression, the following command should do the work.
model = LogisticRegression(random_state=0).fit(X, Y)
To check for a particular value, the command is:
>>model.predict(X[:3, :]) >>array([0, 0, 0])
This specifies that the flowers (performs a query for the last three elements in the array.) under consideration belongs to the class label 0. For specific names, middle layer manipulation can be used.
To check for the probability of occurrence, the following command is used:
>>clf.predict_proba(X[:3, :])
>> array([[8.78030305e-01, 1.21958900e-01, 1.07949250e-05],
[7.97058292e-01, 2.02911413e-01, 3.02949242e-05],
[8.51997665e-01, 1.47976480e-01, 2.58550858e-05]])
This provides the probability of a particular output belonging to a particular class aka provides the probability estimates for the quires.
The regression score can be verified using the following query:
>>model.score(X, y) >>0.96
Logistic regression is a type of binary classification algorithm. Thus, it needs that only two classes are given to it at a time. The other requirement of logistic regression is that it has to be provided with linearly seperable classes for accuracy to be achieved. In case, the classes are not linearly seperable, the accuracy of this classifier can take a hit. Few real-life scenario’s where we use logistic regression is utilized are as follow:
Logistic regression has found its use in numerous scenarios where the classes had been linearly separable. The reasons for the broad fan base are the ease of use and efficiency in terms of computational resources required as well as interpretability of the inherit structure being used. Logistic regression is not in need of scaling the input vector or tuning. This algorithm is easy to regularize and the output generated is in tune with the predicted class probabilities.
Read: How Effective is the Graphics in R?
Logistic regression though requires one to remove the attributes which are not related to the output classes. This is somewhat similar to what is required to be done in linear regression as well. Thus, use of feature extraction is quite evident in the use of this algorithm. In the domain of classification, logistic regression is one of the basic algorithms and thus, extremely easy to train and deploy.
Because of the inherit simplicity and rapid prototyping logistic regression, logistic regression forms the baseline for measuring the space and time complexity of much more complex machine learning algorithms.
Even though the logistic regression is extremely simple to use and implement. It suffers from drawbacks as well. One of the biggest drawback is the requirement of linear separability in the classes being introduced. Also, logistic regression is a binary classifier, thus, in its inherit design it won’t be able to design and handle more than 2 classes.
Conclusion:
In this blog, we have defined the basis of a binary classifier named as Logistic Regression. The blogs throw light on the importance of logistic regression in probability-based classification. Also, this blog brings to light the use advantages and disadvantages of the same algorithm. Here, the situations logistic regression is utilized are being answered. This algorithm can be used in a situation where the probability of occurrence is important.
Please leave the query and comments in the comment section.
FaceBook
Twitter
LinkedIn
Pinterest
Email
A dynamic, highly professional, and a global online training course provider committed to propelling the next generation of technology learners with a whole new way of training experience.
Cyber Security
QA
Salesforce
Business Analyst
MS SQL Server
Data Science
DevOps
Hadoop
Python
Artificial Intelligence
Machine Learning
Tableau
Search Posts
Related Posts
Discover Opportunities: Top 15 Best Data Science Companies Hiring in 2024
396
How to Build a Successful Career in Data Science - A Complete Data Science Career Guide
3.1k
The Best Data Science Projects (Beginner To Advanced)
4.8k
Random Forest: An Easy Explanation of the Forest
4.9k
What Qualifications Are Required To Become Data Scientist?
807.5k
Receive Latest Materials and Offers on Data Science Course
Interviews
May 14, 2024
396
