Various Methods of Constrained Clustering in Data Science

Clustering is a popular technique used in data science to group similar objects together based on their characteristics. However, traditional clustering algorithms do not always take into account certain constraints or prior knowledge about the data that may be available. This can lead to suboptimal results and inaccurate conclusions. In this blog post, we will explore methods for clustering with constraints, also known as constraint based clustering or constrained clustering.

While constrained clustering can be useful in many applications where prior knowledge or domain expertise can inform how data should be grouped, it's important to note that incorporating too many or overly complex constraints can also lead to overfitting and poor generalization performance. Let's dive more into the topic of methods for clustering with constraints and learn more about their importance in data mining and key takeaways. You should check out the data science certifications course to clarify your basic concepts. 

What are The Constraints in Clustering?

Constraints refer to any additional information that can guide the clustering process toward more meaningful and accurate results. These constraints could include domain-specific knowledge, expert opinions, or external datasets that provide supplementary information about the objects being clustered. By incorporating these constraints into the algorithm, we can ensure that the resulting clusters are more relevant and useful.

Constraints play a crucial role in clustering as they help to overcome the limitations of traditional unsupervised clustering algorithms. In many cases, these algorithms rely solely on mathematical computations and assumptions about the data without considering any external factors that could impact the results. Constraints can provide additional information that helps to refine and improve the clustering process.For example, let's say we want to cluster customer data based on their purchasing behavior. We may have some prior knowledge or domain-specific expertise that customers often purchase certain products together. By incorporating this constraint into our algorithm, we can guide it towards creating clusters where customers who purchase those specific products are grouped together.

Another way constraints can be used is through expert opinions or annotations provided by human annotators. These experts may have more detailed knowledge about the objects being clustered than what is available from the data itself. For instance, in medical image analysis, radiologists may provide annotations indicating which regions of an image contain tumors or abnormalities. Incorporating these annotations as constraints can lead to better clustering outcomes because they provide additional context and insight into how different groups should be defined.External datasets can also serve as valuable sources of constraints for clustering tasks. For instance, suppose we're trying to cluster news articles based on their content and topic similarity; in that case, we might incorporate supplementary metadata such as publication date or author name from external databases like Wikipedia or Google News Archive.

In summary, constraints offer a powerful tool for improving clustering accuracy and relevance by providing additional information beyond what is contained within raw data alone. Whether drawing upon domain-specific expertise or leveraging external datasets, incorporating constraints allows us to create more meaningful groupings that reflect real-world phenomena accurately.

Types of Constrained  Clustering

Several types of constraints can be incorporated into a clustering algorithm:

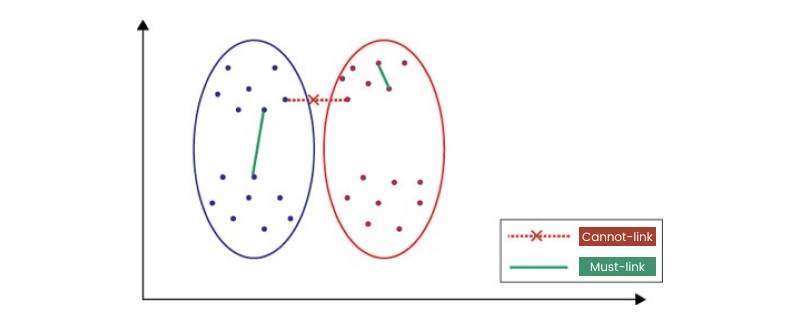
1. Must-Link and Cannot-Link Constraints: 

Must-link constraints specify that two data points must be assigned to the same cluster, while cannot-link constraints specify that two data points should not belong to the same cluster. These constraints are useful when there is prior knowledge about which objects should or should not belong in a particular group. For example, we are clustering customer data for a marketing campaign. In that case, we might want to ensure that customers who have previously made purchases together are clustered in the same group.

2. Attribute Similarity/Dissimilarity:

Attribute similarity or dissimilarity specifies how similar (or dissimilar) two attributes should be within a cluster. This type of constraint can help ensure that clusters contain objects with similar characteristics or features. For example, we cluster images based on their color and texture attributes. In that case, we might want to use attribute similarity as a constraint so that images with similar colors and textures will be grouped together.

3. Cluster Size/Shape:

Cluster size and shape refer to how many objects should be included in each cluster and what shape they should take, respectively. Constraints on cluster size help ensure that each group has roughly equal numbers of members, while constraints on shape can force clusters into specific geometrical shapes like circles or rectangles.

4. Hierarchical Structure:

Hierarchical structure refers to whether certain clusters should be nested within others at different levels of granularity (i.e., sub-clusters). This type of constraint allows us to create hierarchical structures where smaller groups are nested within larger ones based on commonalities between them.Lastly, incorporating different types of constraints into clustering algorithms helps us produce more accurate results by guiding the grouping process according to our prior knowledge or preferences for how data points should be clustered based on their similarities and differences across various dimensions, such as attributes or hierarchies.

Constrained K-Means Algorithm

The K-means algorithm is a popular unsupervised learning technique that groups data points into clusters based on their similarity. However, traditional K-means does not consider any constraints or prior knowledge about the data when clustering. This can lead to suboptimal results in certain situations where there are known relationships or conditions among the data.The constrained K-means algorithm addresses this issue by incorporating additional steps to ensure that the final clusters adhere to specific constraints. These constraints can be hard or soft and are typically defined by domain experts or prior knowledge about the dataset.Hard constraints are strict rules that must be followed, such as ensuring that certain data points belong together in a cluster. Soft constraints, on the other hand, allow some flexibility and aim to encourage certain clustering outcomes without strictly enforcing them.

To incorporate these constraints into K-means, an additional step is added after each iteration of assigning centroids and updating cluster assignments. In this step, all current assignments are checked against the given set of constraints. If any violations are found, adjustments are made before proceeding with another iteration of centroid assignment and reassignment.For example, suppose we have a dataset containing customer information for an e-commerce site consisting of a purchase history (e.g., product categories purchased) and demographic information (e.g., age range). Suppose we aim to segment customers based on their purchasing behavior while ensuring that customers within similar age ranges belong together in separate clusters.

We could define two hard constraints: 

1) Customers within each age range must belong together in one cluster

2) No more than five categories should be included in each cluster to avoid over-segmentation.

Incorporating these hard constraints using constrained K-means would ensure that our resulting clusters satisfy both requirements simultaneously while still optimizing for maximum intra-cluster similarity and minimum inter-cluster distance between centroids.

Overall, constrained K-means offers a powerful tool for clustering datasets with known constraints or prior knowledge. It can help ensure that the resulting clusters are more meaningful, interpretable, and useful for downstream analysis tasks.

Spectral Clustering With Constraints

Another method for constraint based clustering is spectral clustering with constraints. This algorithm uses the spectral decomposition of a similarity matrix to group objects together. By incorporating constraints into this process, we can ensure that the resulting clusters are more meaningful and relevant.Spectral clustering with constraints is a powerful technique that can be used to group objects based on their similarities. In this method, we start by constructing a similarity matrix that captures the pairwise similarities between all objects in the dataset. This matrix is then decomposed using spectral techniques to obtain a set of eigenvectors and eigenvalues.The eigenvectors and eigenvalues obtained from the decomposition are used to create new features for each object, which are then clustered using traditional clustering algorithms like K-means or hierarchical clustering. However, when incorporating constraints into this process, we modify the similarity matrix such that it reflects our prior knowledge about how certain objects should be grouped together.For instance, we have two sets of data points, A and B, but we know beforehand that they belong to different clusters. We can add this constraint by setting the corresponding entries in the similarity matrix to zero or some large negative value so that these points cannot be assigned to the same cluster.

Similarly, suppose we have prior knowledge about which data points must belong together in a particular cluster (known as "must-link" constraints). In that case, we can incorporate them into our algorithm by increasing the similarity values between those data points.Conversely, suppose pairs of data points cannot belong in any cluster (called "cannot-link" constraints). In that case, their corresponding entries in the similarity matrix can be set to zero or some large negative value so that they will not be assigned together during clustering.By incorporating these types of constraints into spectral clustering algorithms, we ensure that our resulting clusters are more meaningful and relevant because they adhere more closely to our prior knowledge about how objects should be grouped together. This makes spectral clustering with constraints an essential tool for many applications where accurate grouping is critical -such as image segmentation or social network analysis- offering better results than standard unsupervised methods without any constraining information added.

Applications of Constrained Clustering

Constraint based clustering has many applications in various fields, such as biology, finance, and marketing. Here are a few examples of constraint based clustering applications: 

• In bioinformatics, researchers may use must-link constraints to group genes with similar functions together. Analysts may use attribute similarity constraints to identify stocks with similar risk profiles for portfolio optimization in finance.
• In addition to the aforementioned applications, constraint based clustering also has uses in image and video processing. For instance, in image segmentation, one may use must-link constraints to group pixels with similar color values together as a single object. This can be useful for identifying objects of interest in an image or separating foreground from background.
• Another application is social network analysis, where attribute similarity constraints can help identify groups of individuals with similar interests or characteristics. This information can then be used for targeted marketing campaigns or personalized recommendations.
• Moreover, constrained clustering has been applied in anomaly detection, where outliers are identified based on their dissimilarity with respect to the rest of the data points while satisfying certain constraints such as minimum cluster size or maximum distance between clusters.
• One important consideration when using constraint based clustering is that it requires prior knowledge about the data and domain expertise to define appropriate constraints. Moreover, adding too many constraints may lead to overfitting and reduce the effectiveness of clustering.
• To overcome these challenges, researchers have developed several methods for semi-supervised constrained clustering that balance incorporating additional information while still allowing some flexibility within the algorithm. These methods include soft constraints, which assign penalties instead of strict rules for violating a constraint, and active learning approaches, which iteratively select informative samples for labeling during training.

Data Science Training For Administrators & Developers

• No cost for a Demo Class
• Industry Expert as your Trainer
• Available as per your schedule
• Customer Support Available

Enroll for Demo Class

Conclusion

Clustering with constraints is an important technique in data science that allows us to incorporate additional information into the clustering process for more accurate results. Several methods are available for constraint based clustering, including constrained K-means and spectral clustering with constraints. With its wide range of applications across different industries and domains, it's clear that constraint based clustering will continue to be an important tool for data scientists moving forward. Understanding methods for clustering with constraints in data mining begins with understanding data science; you can get an insight into the same through our data science training.