Solving The XOR Problem

Deep Feedforward Networks, particularly in the context of the XOR Neural Network, provide a fascinating exploration into the capabilities and limitations of neural networks. The seemingly simple XOR problem has been crucial in developing neural network architectures, specifically deep feedforward networks. This blog aims to dissect the intricacies of learning the XOR function using these networks, highlighting key concepts and methodologies in deep learning training.

The XOR Challenge

The XOR problem is a fundamental concept in the study of neural networks. It involves a simple operation: the XOR function takes two binary inputs and returns 1 if exactly one of the inputs is 1; otherwise, it returns 0. This function poses a unique challenge—it represents a pattern that cannot be linearly separated, making it impossible for a simple perceptron, a feedforward network, to learn the XOR function.

Deep Feedforward Networks: An Overview

Deep feedforward networks, or multilayer perceptrons, are the quintessential architecture in deep learning training. These networks are designed to approximate a function by mapping a set of inputs to outputs. The core of these networks lies in their layer structure, comprising an input layer, multiple hidden layers, and an output layer. Each layer consists of units or neurons that apply an activation function to the weighted sum of its inputs.

XOR in Feedforward Networks

To address the XOR problem, a feedforward neural network must transform the input space into a feature space where the XOR function is linearly separable. This transformation is achieved through the hidden layers of the network. For instance, a simple three-layer neural network can effectively model the XOR function. The network might have two inputs, a hidden layer with two nodes, and a single-node output layer. In this architecture, the first layer's neurons act as feature detectors, transforming the input space into a form where a linear model in the subsequent layers can separate the XOR classes.

Training the Neural Network XOR

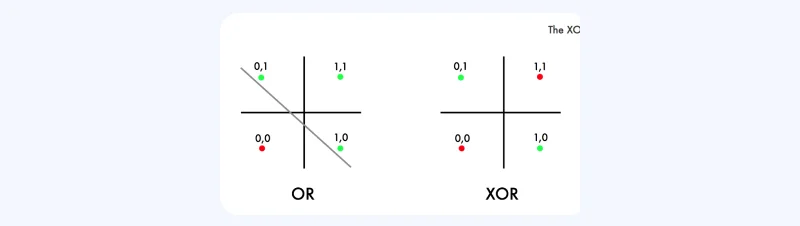
Training a deep feedforward network on the XOR problem involves several critical steps and choices. Firstly, the network is trained on all possible input combinations for the XOR function. The loss function plays a pivotal role in this process. While mean squared error (MSE) is a common choice, especially when treating the problem as a regression, it's not always suitable for binary data. Cross-entropy loss is often preferred due to its efficiency in handling classification problems and compatibility with gradient-based learning.

Activation Functions and Their Importance

The choice of activation functions in the network significantly influences its learning capability. Classic activation functions like sigmoid and hyperbolic tangent have been traditionally used. However, they have limitations due to their saturating nature, which can lead to vanishing gradients—a situation where the gradient becomes too tiny, impeding effective learning. The Rectified Linear Unit (ReLU) and its variants have become popular due to their non-saturating nature and efficiency in promoting faster convergence in deep networks.

The Role of Backpropagation

Backpropagation is a fundamental algorithm in training deep feedforward networks. It involves the propagation of the error gradient back through the network, allowing for efficient computation of gradients for each parameter. This process is essential for updating the weights in the network using gradient descent or its variants, thereby minimizing the loss function.

The Universal Approximation Theorem

A pivotal concept in understanding deep feedforward networks is the Universal Approximation Theorem. It states that a feedforward network with a single hidden layer containing a finite number of neurons can approximate any continuous function on compact subsets of R^n, given appropriate weights and biases. This theorem underscores the potential of deep feedforward networks to tackle a wide range of problems, including the XOR problem.

Practical Considerations

In real-world scenarios, implementing a neural network to solve the XOR problem or similar challenges requires careful consideration of various factors. These include the number of hidden layers and units, the type of activation functions, the optimization algorithm, and the regularization techniques. Regularization, such as dropout or L2 regularization, helps prevent overfitting, a common issue in deep learning models.

Challenges in Training Deep Feedforward Networks for XOR

While deep feedforward networks can theoretically solve the XOR problem, several challenges arise during training:

1. Vanishing Gradients: In deep networks with many layers, the gradients can become extremely small during backpropagation. This issue, known as vanishing gradients, makes it difficult for the network to learn effectively, especially when using activation functions like sigmoid or hyperbolic tangent. The choice of activation functions, such as ReLU, can mitigate this problem.

2. Exploding Gradients: Conversely, gradients can also become extremely large, leading to exploding gradients. This can cause the network to diverge during training. Gradient clipping is a common technique used to address this issue.

3. Initialization: Proper initialization of network weights is crucial for training deep networks. Methods like Xavier/Glorot initialization and He initialization have been developed to ensure that weights are initialized in a way that facilitates learning.

4. Overfitting: Deep networks are prone to overfitting, where they memorize the training data instead of generalizing from it. Regularization techniques like dropout and L2 regularization are essential to combat overfitting.

Modern Solutions to the XOR Problem

In recent years, researchers have developed more advanced architectures and techniques to tackle the XOR problem with deep feedforward networks:

1. Residual Networks (ResNets): ResNets introduce skip connections or residual blocks, allowing gradients to flow more easily during training. This architecture has been successful in training intense networks.

2. Batch Normalization: Batch normalization normalizes the activations in each layer, reducing internal covariate shifts and helping networks converge faster. It has become a standard component in deep network architectures.

3. Learning Rate Schedules: Dynamic learning rate schedules, such as learning rate decay, can help training convergence. These schedules reduce the learning rate during training, allowing the model to fine-tune as it approaches a solution.

4. Advanced Optimization Algorithms: Modern optimization algorithms like Adam and RMSprop have proven effective in training deep networks, offering advantages over traditional gradient descent.

Deep Learning Training and Courses

For those keen on delving deeper into deep learning and neural networks, numerous top deep learning courses online offer comprehensive training. These courses cover fundamental concepts, practical implementations, and advanced topics, providing a solid foundation for understanding and applying deep learning techniques in various domains.

Conclusion

The XOR neural network exemplifies the complexities and capabilities of deep feedforward networks. Through careful architecture design, choice of activation functions, and training methods, these networks can effectively learn and generalize from data, solving problems once deemed insurmountable. As deep learning continues to evolve, its applications in solving real-world problems expand, making it an exciting and ever-relevant field of study.