Introduction To Data Cube Computation And It’s Types

Data science is a rapidly growing field that deals with the extraction of insights and knowledge from data. One of the most important tools used by data scientists is the data cube, which allows them to analyze large datasets and extract valuable information. In this blog post, we will explore what data cubes are, how they are used in both data warehousing and mining, and various methods for computing them. For an in-depth understanding of data cube computation, our Data scientist course online helps you explore more about cube computation data mining, the most effective tool of data science.

What is a Data Cube?

A Data cube can be defined as a multi-dimensional array that stores aggregated information about different aspects of a dataset. It provides an efficient way to summarize large amounts of information into smaller sets that can be easily analyzed. The dimensions in a data cube represent different attributes or variables within the dataset while each cell contains an aggregate value such as sum, count or average.

Data Cube in Data Mining

In contrast to OLAP cubes created for business intelligence purposes, those created for mining purposes focus on discovering hidden patterns within datasets rather than simply summarizing it. These types of cubes are often referred to as Concept Hierarchies because they group similar items together based on shared characteristics or behaviors.Data cube computation is the process of transforming raw data into multidimensional views, or "cubes," for efficient analysis and exploration. By organizing data into dimensions and measures, data cube computation enables users to drill down or roll up data, filter and group data based on various criteria, and identify trends and patterns that may not be visible in traditional reports. 

Data cube computation is a critical component of data warehousing and business intelligence, enabling organizations to unlock the insights hidden within their data and gain a competitive edge in the marketplace.You can learn more about data computation and other data science concepts with a data science tutorial. This blog post provides an introduction to data cube computation and its benefits for data warehousing and business intelligence.  

What is Data Cube Computation?

Data cube computation is an important step in the process of creating a data warehouse. Depending on your requirements, full or partial data cube pre-computation can greatly improve the reaction time and performance of online analytical processing. Performing such a computation, however, may be difficult because it may take a significant amount of time and room on the computer. Multidimensional data can be examined in real-time using data cubes. The process of shifting a significant amount of information in a database that is relevant to a particular job from a low level of abstraction to a higher one is known as Data Generalization. It is extremely helpful and convenient for users to have large data sets depicted in simple terms, at varied degrees of granularity, and from a variety of perspectives. This saves users a great deal of time. These kinds of data summaries are helpful because they provide a picture that encompasses the entire set of facts. 

Through the use of cube in data warehouse and Online Analytical Processing (OLAP), one can generalize data by first summarizing it at multiple different levels of abstraction. In this blog we will understand the techniques and strategies used in data cube computation. You can learn more about data cube computation in detail along with other data science and data mining concepts with an online data science course.For example, a retail company may use a data cube to analyze their sales data across different dimensions such as product categories, geographical locations, and time periods. By doing so, they can identify which products are selling the most in specific regions or during certain times of the year. This information can then be used to make more informed decisions about inventory management and marketing strategies.

Data Cube in Data Mining

In addition to its use in data warehousing, data cubes also play an important role in data mining. Data mining is the process of discovering patterns and relationships within large datasets that cannot be easily identified through manual analysis. One common technique used in data mining is association rule mining which involves identifying co-occurring items within a dataset.

A Data Cube makes it easier to perform association rule mining by allowing analysts to group items based on multiple dimensions simultaneously. For example, an e-commerce website may use a data cube to analyze customer transactional records across different dimensions such as product categories, customer demographics, and purchase frequency. By doing so, they can identify which products are frequently purchased together by specific groups of customers.

Methods For Data Cube Computation?

1) Materialization of Cube: Full, Iceberg, Closed and Shell Cubes 

A three-dimensional data cube with dimensions A, B, and C and an aggregate measure M. You can think of a data cube as a lattice of cuboids. Each cube is meant to symbolize a group.  The fundamental cuboid, encompassing all three dimensions, is the ABC. The aggregate measure (M) is calculated for each permutation of the three dimensions. There are six different cuboids that make up a data cube, with the base cuboid being the most specific. The apex cuboid is the most generalized cuboid. It stores a single number - the sum of all the tuples' measures in the base cuboid's measure M. From the topmost cuboid of the data cube example, we can descend into the lattice to access deeper levels of information.

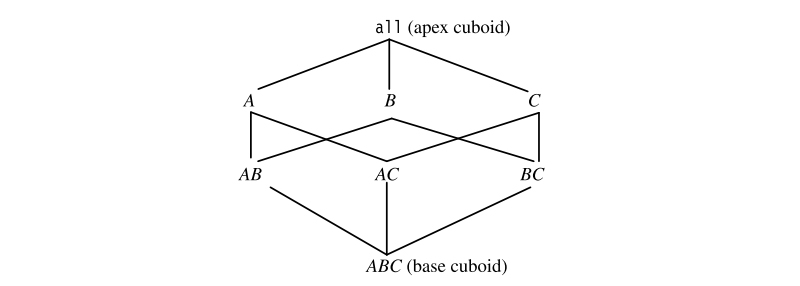
Lattice of cuboids that make  upa 3-D data cube with A, B, C dimensions for an aggregate measure M (Image Source: Data Mining: Concepts and Techniques - Han and Kamber)When rolling up, one begins at the bottom cube and works one's way up. For the rest of this chapter, whenever we speak to a data cube definition, we mean a lattice of cuboids rather than a single cuboid.

Base Cell In Data Cube

The term "base cell" refers to a cell in the base cuboid. Aggregate cells are cells that are not based on a cube. Each dimension that is aggregated in an aggregate cell is represented by a "" in the cell notation. Let's pretend we're working with an n-dimensional data cube. Let each cell of the cuboids that make up the data cube be denoted by a = (a1, a2,..., an, measurements). If there are m (m n) values of a, b, c, d, e, f, g, h, I j, k, l, m, n, and o that are not "," then we say that an is an m-dimensional cell (that is, from an m- A is a base cell if and only if m = n; otherwise, it is an aggregate cell (where m n).

On occasion, it is desirable to precompute the whole cube to ensure rapid on-line analytical processing (i.e., all the cells of all of the cuboids for a given data cube). The complexity of this task, however, grows exponentially with the number of dimensions. In other words, there are 2n cuboids inside an n-dimensional data cube. When we include in the concept hierarchies for each dimension, the number of cuboids grows much larger. 1Additionally, the size of each cuboid is determined by the cardinality of its dimensions. Therefore, it is not uncommon for precomputation of the whole cube to necessitate vast and frequently excessive quantities of memory. Still, algorithms that can calculate a whole cube are crucial. Secondary storage can be used to keep individual cuboids out of the way, until they're needed. Alternatively, we can use these techniques to compute cubes with fewer dimensions, or dimensions with narrower ranges of values. For some range of dimensions and/or dimension values, the smaller cube is a complete cube.We can create effective methods for computing partial cubes if we have a firm grasp on how whole cubes are computed. Therefore, it is crucial to investigate scalable approaches for fully materializing a data cube, i.e., calculating all of the cuboids that comprise it. These techniques need to think about the time and main memory constraints associated with cuboid calculation, as well as the total size of the data cube that will be computed.

Cuboids In Data Cube

As an intriguing compromise between storage requirements and response times for OLAP, data cubes that are partially materialized are a viable option. We cannot compute the entire data cube, but rather only parts of it, called cuboids, each of which is composed of a subset of the cells in the full cube.

Data analysts may find that many cube cells contain information that is of little use to them. You may recall that a complete cube's cells all contain summative values. Numbers, totals, and monetary sales figures are popular units of measurement. The measure value for many cuboid cells is zero. We say that a cuboid is sparse when the number of non-zero-valued tuples stored in it is small compared to the product of the cardinalities of the dimensions stored in it. One defines a cube as sparse if it is made up of several sparse cuboids.A huge number of cells with extremely small measure values can take up a lot of room in the cube. This is due to the fact that cube cells in an n-dimensional space are typically relatively spread out. In a store, a consumer might only buy a few goods at a time. It's likely that this kind of thing would only produce a handful of full cube cells. When this occurs, it can be helpful to only materialize the cuboid cells (group-by) whose measure value is greater than a predetermined threshold. Say we have a data cube for sales, and we only care about the cells where the count is greater than 10 (i.e., when at least 10 tuples exist for the cell's given combination of dimensions), or the cells where the sales amount is greater than $100. 

Minimum Support And Iceberg In Data Cube

Not only does this result in a more effective utilization of resources (namely, CPU time and disc space), but it also makes it possible to conduct more accurate analysis. There is a good chance that the non-passing cells are not important enough to warrant further investigation. Cubes that only partially materialize are referred to as iceberg cubes, and this phrase is used to characterize such cubes. The term "minimum support," also abbreviated as "min sup" for short, describes the criteria that are the absolute minimum acceptable. It is common practise to refer to the effect of materializing only a fraction of the cells in a data cube as the "tip of the iceberg." In this context, "iceberg" refers to the entire cube including all cells.

A naïve technique to computing an iceberg cube would be to first calculate the full \scube and then prune the cells that do not satisfy the iceberg requirement. However, this is still unreasonably expensive. To save time, it is possible to compute simply the iceberg cube directly instead of the whole cube. The introduction of iceberg cubes simplifies the computation of inconsequential aggregate cells in a data cube. Nonetheless, it is possible that we will have a significant number of boring cells to process.

The idea of closed coverage needs to be introduced if we are to compress a data cube in a systematic manner. If there is no cell d such that d is a specialization (descendant) of c (obtained by substituting a in c with a non- value) and d has the same measure value as c, then c is said to be closed. All of the cells in a data cube are considered closed in a closed cube. For the data set [(a1, a2, a3,..., a100): 10], the three cells [(b1, b2, b3,..., b100): 10][[a1, b2, b3,..., b100]] are the three closed cells of the data cube. They make up the lattice of a closed cube, from the equivalent closed cells in this lattice, other non-closed cells can be constructed. It is possible to infer "(a1, a2, b3,...): 10" from "(a1, a2, b3,...): 10" because "(a1, a2, b3,...): 10" is a generalized non-closed cell of "(a1, a2, b3,...): 10".As another method of partial materialization, precomputing only the cuboids involving a small number of dimensions, say, 3 to 5, is feasible. When placed together, these cuboids create a cube shell around the associated data cube. Any more dimension-combination queries will require on-the-fly computation. In an n-dimensional data cube, for instance, we could compute all cuboids of dimension 3 or smaller, yielding a cube shell of dimension 3. 

Three closed cells forming the lattice of a closed cube   (Image Source: Data Mining: Concepts and Techniques - Han and Kamber) However, when n is large, this can still lead to a very large number of cuboids to compute. Alternatively, we can select subsets of cuboids of interest and precompute only those subshells. Such shell fragments and a method for computing them are discussed in.

2) Roll-up/Drill-down- This method involves aggregating data along one or more dimensions to create a summary of the dataset. It can be used to drill-down into specific areas of interest within the data. Roll-up/Drill-down is useful for quickly summarizing large datasets into manageable chunks while still maintaining important information about each dimension. For example, if you have sales data for multiple products across several regions, you could use roll-up/drill-down to see total sales across all regions or drill-down into sales numbers for one particular product in one region.

3) Slice-and-Dice - This method involves selecting subsets of data based on certain criteria and then analyzing it using different dimensions. It is useful for identifying patterns that may not be immediately apparent when looking at the entire dataset.Slice-and-Dice allows users to select subsets of data based on specific criteria such as time period or customer demographics which can then be analyzed using different dimensions like product categories or geographic locations. This helps identify patterns that may not be immediately apparent when looking at the entire dataset.

4) Grouping Sets - This method involves grouping data by multiple dimensions at once, allowing for more complex analysis of the dataset.Grouping Sets are useful when analyzing large datasets with multiple dimensions where users want to group by two or more dimensions at once. For example, grouping sets could show total revenue broken down by both product category and region simultaneously.

5) Online Analytical Processing (OLAP) - This method uses a multidimensional database to store and analyze large amounts of data. It allows for quick querying and analysis of the data in different ways.OLAP databases are specifically designed for analyzing large amounts of multi-dimensional data quickly through pre-aggregated values stored in memory making it ideal for real-time decision-making scenarios like stock market analysis.

6) SQL Queries - SQL queries can be used to compute data cubes by selecting specific columns and aggregating them based on certain criteria. This is a flexible method that can be customized based on the needs of the user.SQL queries provide flexibility regarding how much control users have over what they want from their cube as well as customization options such as adding additional calculations or filtering data based on specific criteria. SQL queries are ideal when users have a good understanding of the underlying dataset and want to customize their analysis in real-time.

Materialized Views are useful when dealing with small datasets or when computing time isn't an issue. However, as datasets become larger and more complex, materializing views becomes less feasible due to storage limitations and computation time.

Data Science Training For Administrators & Developers

• No cost for a Demo Class
• Industry Expert as your Trainer
• Available as per your schedule
• Customer Support Available

Enroll for Demo Class

Conclusion

It could be difficult to perform a calculation involving cubes on a computer since it could take a long time and require a lot of storage space. Data cubes allow for the instantaneous examination of data with multiple dimensions.When working with a variety of different cube types, it stands to reason that there must be a variety of different computing strategies to choose from. To know about data science and data cube in data mining in depth, you can opt for data science online certification  and pace up with the latest data trends and use.

FAQ’s

1. What are The Benefits of Data Scientist Course Online?

There are various benefits that comes with the data science certification online course. These include a sure advancement in the career path, flexibility and independency of opinions and a wide options to choose from, proper education structure, and smooth demonstration of your skills. The data scientist course online also helps us to grasp the famous data science tools and helps you remain updated on the modern industry advancements.

2. What are The Career Opportunities That Comes With The Online Master Data Science Course?

The online master data science course comes with various career scope. These include pursuing the career as a Data Scientist, Data Analyst, Risk Analyst, or as a Senior Data Analyst. The Data science training online also allows you tot ake the session from the comfort of your home.

3. Can You Define Data Cube in Data Mining?

The data cube in data mining is also termed as a business intelligence cube. To answer the question of what is data cube in data mining, we need to define it first. It is a data structure used for rapid and proper analysis. It allows consolidating and collecting correct data into the cube and then drilling, cutting and pivoting the dat to visualize it from various angles. Hence this is the data cube definition. 

4. Explain What is Data Cube in Data Warehouse?

A data cube in data warehouse refers to a multi-dimensional range of values utilized to assimilate together data to be arranged and structured for analysis. A data warehouse refers to the database where data is stored and made ready for decision-making process. Hence this refers to a data cube in data warehouse. 

5. Can You Specify a Cube in Data Warehouse With Example?

A data cube refers to a multi-dimensional data algorithm. A data cube is characterized by the dimensions like the product, states, and Date. Every dimension is linked to respective qualities , such as the qualities of the items dimensions are T- shirt, Shirt, Jacket, and Jeans. Hence this is a data cube example.